A természetes geometriai minták vagy minták ismétlődő alakzatokként jelennek meg, amelyek néha matematikai modellekkel leírhatók vagy ábrázolhatók.
A természetben és az életben a geometriának számos formája van, például szimmetria, spirál vagy hullám.
Előzmények
Az ókori görög filozófusok és tudósok - Püthagorasz, Empedoklész és Platón - most először foglalkoztak a természet geometriájával. A növények és állatok kiszámítható vagy ideális geometriai alakzataira példákat elemezve igyekeztek bemutatni a természet rendjét és szimmetriáját.
A természetben a geometria tanulmányozására irányuló modern kísérletek a 19. században kezdődtek Joseph Plateau belga fizikus erőfeszítéseivel, aki kidolgozta a szappanbuborék minimális felületének koncepcióját. Az első modern próbálkozások először az ideális és kiszámítható geometriai alakzatok bemutatására koncentráltak, majd olyan modellek kifejlesztésére irányultak, amelyek előrejelzik a geometria megjelenését és megnyilvánulását a természetben.
A 20. században Alan Turing matematikus a morfogenezis mechanizmusán dolgozott, ami megmagyarázza az állatokban való megjelenéstkülönféle minták, csíkok, foltok. Kicsit később Aristide Lindenmeier biológus Benoit Mandelbrot matematikussal együtt befejezi a matematikai fraktálok kidolgozását, amelyek megismétlik néhány növény, köztük a fák növekedési mintáját.
Tudomány
A modern tudományok (matematika, fizika és kémia) a technológiák és modellek segítségével igyekeznek nem csak megmagyarázni, hanem megjósolni is a természetben fellelhető geometriai mintákat.
Sok élő szervezet, például a páva, a kolibri és a tengeri kagyló alakja és színe nemcsak szép, hanem geometriailag is helyes, ami felkelti a tudósok kíváncsiságát. A természetben megfigyelt szépség természetes módon, matematikailag előidézhető.
A matematikában megfigyelt természetes mintázatokat a káoszelmélet magyarázza, amely spirálokkal és fraktálokkal dolgozik. Az ilyen minták engedelmeskednek a fizika törvényeinek, emellett a fizika és a kémia az absztrakt matematika segítségével megjósolja a kristályok természetes és mesterséges alakját.
A biológia a természet geometriáját a természetes szelekcióval magyarázza, ahol az olyan szabályos jellemzők, mint a csíkok, foltok, élénk színek a maszkolás vagy a jelek küldésének szükségességével magyarázhatók.
Minták típusai
A természetben számos ismétlődő minta található, amelyek különböző geometriai alakzatokban jelennek meg. A természet geometriájának alapvető szabályszerűségeinek típusait, fényképeket és azok leírását az alábbiakban találja.
Szimmetria. Ez a geometriai forma az egyik leggyakoribb a természetben. Leggyakrabban állatokbantükör szimmetria - pillangók, bogarak, tigrisek, baglyok. Növényekben is megtalálható, például juharlevelekben vagy orchidea virágokban. Ezenkívül a természetben a szimmetrikus geometria lehet sugárirányú, ötsugaras vagy hatszoros, mint a hópelyhek.

Fraktálok. A matematikában ezek önhasonló konstrukciók, amelyek végtelenek. A természetben lehetetlen ilyen végtelenül ismétlődő formát észlelni, ezért a fraktálmintázatok közelítését a természetben geometriai fraktáloknak nevezik. Ilyen geometria figyelhető meg a természetben a páfránylevélben, a brokkoliban, az ananászban.
Spirálok. Ezek a formák különösen a puhatestűek és a csigák körében gyakoriak. A tudósok spirális alakzatokat figyelnek meg az űrben, például spirálgalaxisokat. A spirált Fibonacci aranymetszésének nevezik.

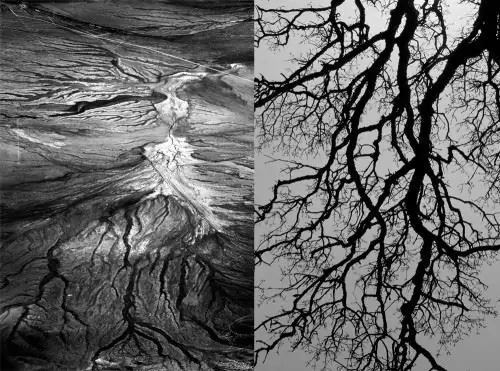
Meanders. A matematikai dinamikus rendszerek véletlenszerűsége a természetben kanyarulatokban és áramlásokban nyilvánul meg. A természetes geometria szaggatott vagy inkább ívelt vonal, például folyó áramlása.
Hullámok. Ezeket a levegő zavarai és mozgása, széláramlatok okozzák, amelyek levegőn és vízen is terjednek. A természetben ezek nemcsak tenger hullámai, hanem sivatagi dűnék is, amelyek geometriai formákat - vonalakat, félholdakat és parabolákat - alkothatnak.
Mozaik. Ugyanazoknak az elemeknek a felületen történő ismétlésével készült. A vadon élő állatok mozaikgeometriája a méhekben található: építenekméhsejt kaptár - ismétlődő sejtek.

Minták kialakítása
A biológiában a geometriai szín kialakulása a természetes kiválasztódás folyamatának köszönhető. A 20. század közepén Alan Turingnak sikerült leírnia az állatok színében megjelenő foltok és csíkok megjelenésének mechanizmusát - ezt reakció-diffúziós modellnek nevezte. A test bizonyos sejtjei olyan géneket tartalmaznak, amelyeket kémiai reakciók szabályoznak. A morfogén sötét pigmenttel rendelkező bőrterületek kialakulásához vezet (foltok és csíkok). Ha a morfogén minden bőrsejtben jelen van - megkapjuk a párduc színét, ha egyenlőtlenül van jelen - a szokásos foltos leopárd.






