A rugalmassági modulus egy fizikai mennyiség, amely az anyag rugalmas viselkedését jellemzi, amikor egy adott irányban külső erő hat rá. Az anyag rugalmas viselkedése a rugalmas tartományban bekövetkező deformációját jelenti.
Az anyagok rugalmasságának vizsgálatának története

A rugalmas testek fizikai elméletét és viselkedésüket külső erők hatására részletesen átgondolta és tanulmányozta a 19. századi angol tudós, Thomas Young. A rugalmasság fogalmát azonban már 1727-ben kidolgozta Leonhard Euler svájci matematikus, fizikus és filozófus, és a rugalmassági modulussal kapcsolatos első kísérleteket 1782-ben, azaz 25 évvel Thomas Jung munkája előtt végezték el., Jacopo Ricatti velencei matematikus és filozófus.
Thomas Young érdeme abban rejlik, hogy karcsú, modern megjelenést kölcsönzött a rugalmasság elméletének, amelyet ezt követően egy egyszerű, majd általánosított Hooke-törvény formájában formalizáltak.
A rugalmasság fizikai természete
Bármely test atomokból áll, amelyek között a vonzás és a taszítás erői hatnak. Ezen erők egyensúlya azaz anyag állapota és paraméterei adott körülmények között. A szilárd test atomjai, ha jelentéktelen külső feszítő- vagy összenyomó erőt fejtenek ki rájuk, elkezdenek eltolódni, ellentétes irányú és egyenlő nagyságú erőt hozva létre, amely az atomokat visszaállítja kiindulási állapotába.
Az atomok ilyen elmozdulása során az egész rendszer energiája megnő. A kísérletek azt mutatják, hogy kis alakzatoknál az energia arányos ezen alakzatok négyzetével. Ez azt jelenti, hogy az erő, amely az energiához képest derivált, arányosnak bizonyul az alakváltozás első hatványával, azaz lineárisan függ tőle. Arra a kérdésre válaszolva, hogy mekkora a rugalmassági modulus, azt mondhatjuk, hogy ez az arányossági együttható az atomra ható erő és az erő által okozott deformáció között. A Young-modulus dimenziója megegyezik a nyomás dimenziójával (Pascal).
Elasztikus korlát
A definíció szerint a rugalmassági modulus azt jelzi, hogy mekkora feszültséget kell kifejteni egy szilárd testre ahhoz, hogy alakváltozása 100%-os legyen. Azonban minden szilárd anyag rugalmassági határa 1% alakváltozás. Ez azt jelenti, hogy ha megfelelő erőt alkalmazunk és a testet 1%-nál kisebb mértékben deformáljuk, akkor ennek az erőnek a megszűnése után a test pontosan visszaállítja eredeti alakját és méreteit. Ha túl nagy erőt alkalmazunk, amelynél az alakváltozási érték meghaladja az 1%-ot, a külső erő megszűnése után a test már nem állítja vissza eredeti méreteit. Ez utóbbi esetben maradó alakváltozás létezéséről beszélünk, ami azbizonyíték arra, hogy az anyag rugalmassági határát túllépték.
Young modulusa működés közben
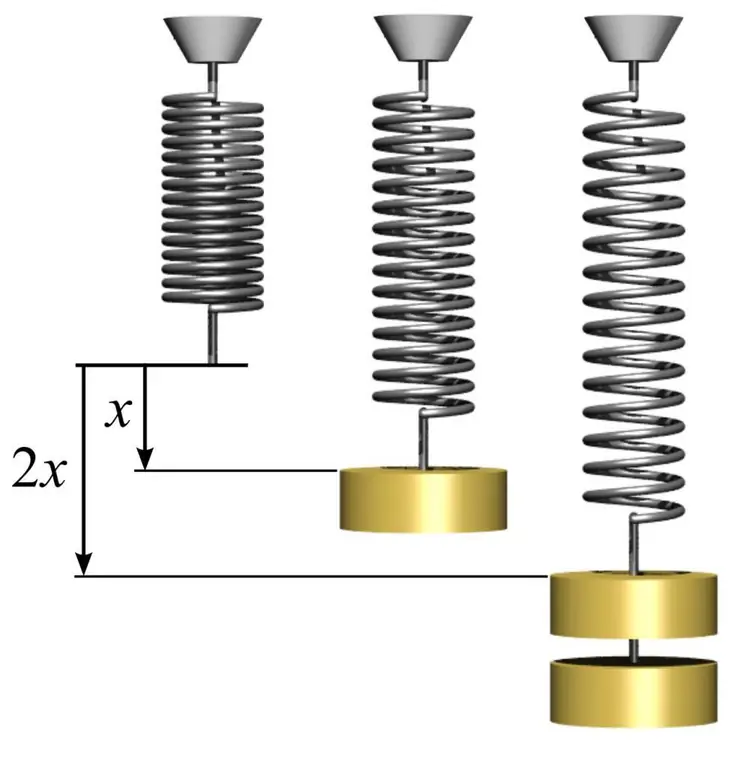
A rugalmassági modulus meghatározásához és használatának megértéséhez adhat egy egyszerű példát egy rugóval. Ehhez vegyen egy fémrugót, és mérje meg a tekercsek által alkotott kör területét. Ez az egyszerű S=πr² képlet segítségével történik, ahol n pi egyenlő 3,14, és r a rugó tekercsének sugara.
Ezután mérje meg a rugó hosszát l0 terhelés nélkül. Ha bármilyen m1 tömegű terhet akasztunk egy rugóra, akkor a hossza egy bizonyos l1 értékre nő. Az E rugalmassági modulus a Hooke-törvény ismeretében a következő képlettel számítható ki: E=m1gl0/(S(l) 1-l0)), ahol g a szabadesési gyorsulás. Ebben az esetben megjegyezzük, hogy a rugó deformációja a rugalmas tartományban jelentősen meghaladhatja az 1%-ot.
A Young-modulus ismerete lehetővé teszi, hogy előre jelezze az alakváltozás mértékét egy adott feszültség hatására. Ebben az esetben, ha egy másik m2 tömeget akasztunk a rugóra, a következő relatív alakváltozást kapjuk: d=m2g/ (SE), ahol d - relatív deformáció a rugalmas tartományban.
Izotrópia és anizotrópia
A rugalmassági modulus egy anyag jellemzője, amely leírja az atomjai és molekulái közötti kötés erősségét, azonban egy adott anyagnak több különböző Young-modulusa is lehet.
A tény az, hogy minden egyes szilárd anyag tulajdonságai a belső szerkezetüktől függenek. Ha a tulajdonságok minden térirányban azonosak, akkor izotróp anyagról beszélünk. Az ilyen anyagok homogén szerkezetűek, így a külső erő különböző irányú hatása rájuk ugyanazt a reakciót váltja ki az anyagból. Minden amorf anyag izotróp, mint például a gumi vagy az üveg.
Az anizotrópia egy olyan jelenség, amelyet a szilárd vagy folyadék fizikai tulajdonságainak az iránytól való függősége jellemez. Minden fémnek és az ezeken alapuló ötvözetnek van egy vagy másik kristályrácsa, vagyis az ionmagok rendezett, nem pedig kaotikus elrendezése. Az ilyen anyagoknál a rugalmassági modulus a külső feszültség hatástengelyétől függően változik. Például a köbös szimmetriájú fémek, például az alumínium, a réz, az ezüst, a tűzálló fémek és mások, három különböző Young-modullal rendelkeznek.
Nyírási modulus
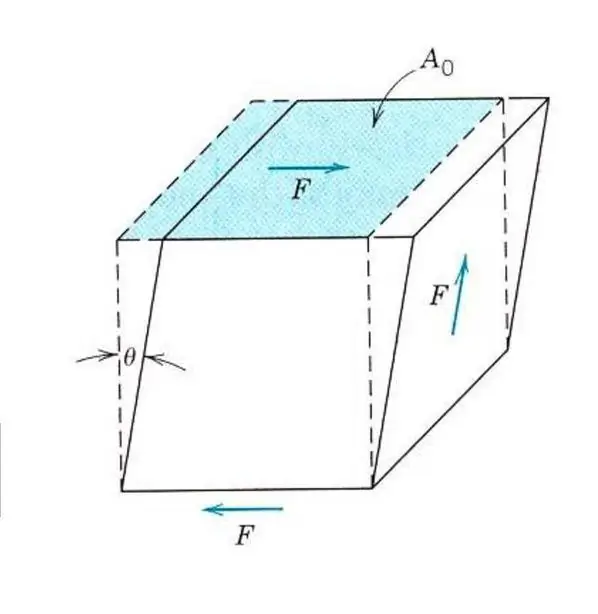
Még egy izotróp anyag rugalmassági tulajdonságainak leírásához sem szükséges egyetlen Young-modulus ismerete sem. Mert az anyagot a feszítés és összenyomás mellett nyírófeszültségek vagy torziós igénybevételek is befolyásolhatják. Ebben az esetben másképp reagál a külső erőre. A rugalmas nyírási alakváltozás leírásához a Young-féle modulus, nyírási modulus vagy a második típusú rugalmassági modulus analógját vezetjük be.
Minden anyag kevésbé ellenáll a nyírófeszültségnek, mint a feszítés vagy a nyomás, ezért a nyírási modulus értéke 2-3-szor kisebb, mint a Young-modulus. Így a titán esetében, amelynek Young-modulusa 107 GPa, a nyírási moduluscsak 40 GPa, az acél esetében ezek a számok 210 GPa, illetve 80 GPa.
A fa rugalmassági modulusa

A fa anizotróp anyag, mivel a farostok meghatározott irányban orientálódnak. A szálak mentén mérjük a fa rugalmassági modulusát, mivel az 1-2 nagyságrenddel kisebb a szálak mentén. A Young-féle fa modulus ismerete fontos, és ezt figyelembe veszik a fa panelszerkezetek tervezésekor.
A fa rugalmassági modulusának értékei egyes fafajtáknál az alábbi táblázatban láthatók.
| Fanézet | Young modulusa a GPa-ban |
| Babérfa | 14 |
| Eukaliptusz | 18 |
| Cédrus | 8 |
| Sluce | 11 |
| Fenyő | 10 |
| Tölgy | 12 |
Megjegyzendő, hogy a megadott értékek egy adott fánál akár 1 GPa-val is eltérhetnek, mivel annak Young-modulusát a fa sűrűsége és a növekedési feltételek befolyásolják.

A nyírási modulusok különböző fafajoknál 1-2 GPa tartományban vannak, például fenyőnél 1,21 GPa, tölgynél pedig 1,38 GPa, vagyis a fa gyakorlatilag nem bírja a nyírófeszültséget. Ezt a tényt figyelembe kell venni a fából készült teherhordó szerkezetek gyártása során, amelyeket úgy terveztek, hogy csak feszítésben vagy nyomásban működjenek.
Fémek rugalmas jellemzői
A fa Young-modulusával összehasonlítva ennek az értéknek a fémekre és ötvözetekre vonatkozó átlagértékei egy nagyságrenddel nagyobbak, amint azt a következő táblázat mutatja.
| Fém | Young modulusa a GPa-ban |
| Bronz | 120 |
| Réz | 110 |
| Acél | 210 |
| Titán | 107 |
| Nikkel | 204 |
A köbös szingoniával rendelkező fémek rugalmas tulajdonságait három rugalmassági állandó írja le. Ilyen fémek a réz, nikkel, alumínium, vas. Ha egy fémnek hatszögletű szingóniája van, akkor már hat állandóra van szükség a rugalmas jellemzőinek leírásához.
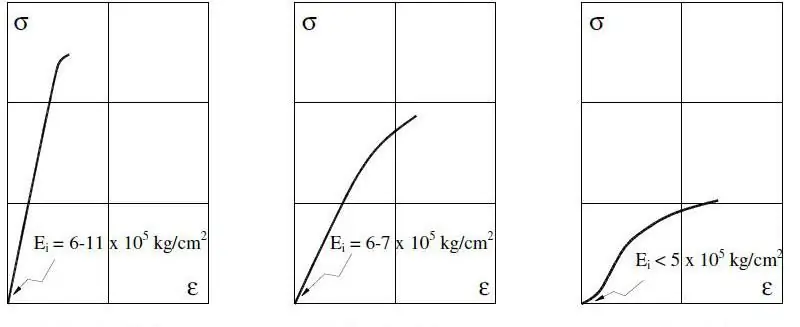
Fémes rendszerek esetében a Young-modulus 0,2%-os alakváltozáson belül van mérve, mivel a rugalmatlan tartományban már nagy értékek is előfordulhatnak.






