Néha úgy tűnik, hogy világunk egyszerű és világos. Valójában ez az Univerzum nagy rejtélye, amely egy ilyen tökéletes bolygót teremtett. Vagy talán olyan valaki készítette, aki valószínűleg tudja, mit csinál? Korunk legnagyobb elméi dolgoznak ezen a kérdésen.

Minden alkalommal arra a következtetésre jutnak, hogy lehetetlen mindent megteremteni, amink van a Legfelsőbb elme nélkül. Milyen rendkívüli, összetett és egyben egyszerű és közvetlen a Föld bolygónk! A minket körülvevő világ csodálatos szabályaival, formáival, színeivel.
A természet törvényei
Az első dolog, amit észrevehet hatalmas és csodálatos bolygónkon, az a tengelyirányú szimmetria. A környező világ minden formájában megtalálható, és egyben a szépség, az idealitás és az arányosság alapelve is. Ez nem más, mint a matematika a természetben.
A "szimmetria" fogalma harmóniát, helyességet jelent. Ez a környező valóság sajátja, rendszerezi a töredékeket és egységes egésszé alakítja őket. Még az ókori Görögországban is először észlelték ennek a törvénynek a jeleit. Például Platón úgy gondolta, hogy a szépség kizárólagosan jelenik mega szimmetria és az arányosság miatt. Valójában, ha olyan tárgyakat nézünk, amelyek arányosak, helyesek és teljesek, akkor a belső állapotunk gyönyörű lesz.
A matematika törvényei az élő és élettelen természetben
Vegyünk egy pillantást bármelyik teremtményre, például a legtökéletesebbre - egy férfira. Látni fogjuk a test felépítését, amely mindkét oldalon ugyanúgy néz ki. Számos mintát is felsorolhat, például rovarokat, állatokat, tengeri élőlényeket, madarakat. Minden fajnak megvan a maga színe.

Ha jelen van bármilyen minta vagy minta, az ismert, hogy a középvonalon tükröződik. Minden élőlény az univerzum szabályai miatt jön létre. Ilyen matematikai minták nyomon követhetők az élettelen természetben.
Ha minden jelenségre odafigyelsz, mint például a tornádó, a szivárvány, a növények, a hópelyhek, sok közös vonást találhatsz bennük. Ami a szimmetriatengelyt illeti, a fa levele ketté van osztva, és mindegyik rész az előző tükre lesz.

Ha egy függőlegesen emelkedő tornádót hozunk példának, és úgy néz ki, mint egy tölcsér, akkor az is feltételesen osztható két teljesen azonos félre. A szimmetria jelenségével a nappal és az éjszaka, az évszakok változásában találkozhatsz. A környező világ törvényei a természetben a matematika, amelynek megvan a maga tökéletes rendszere. Az Univerzum teremtésének egész koncepciója ezen alapul.
Szivárvány
Ritkán gondolunk természeti jelenségekre. Havazott vagy esett, kinézettlesütött a nap vagy mennydörgés - a változó időjárás szokásos állapota. Vegyünk egy többszínű ívet, amely általában csapadék után található. A szivárvány az égen elképesztő természeti jelenség, amelyet csak az emberi szem számára látható színspektrum kísér. Ez annak köszönhető, hogy a napsugarak áthaladnak a kilépő felhőn. Minden esőcsepp optikai tulajdonságokkal rendelkező prizmaként szolgál. Azt mondhatjuk, hogy minden csepp egy kis szivárvány.

A vízzáron áthaladva a sugarak megváltoztatják eredeti színüket. Minden fénysugárnak van egy bizonyos hossza és árnyalata. Ezért a szemünk a szivárványt olyan sokszínűnek érzékeli. Vegye figyelembe azt az érdekes tényt, hogy ezt a jelenséget csak egy személy láthatja. Mert ez csak egy illúzió.
Szivárványtípusok
- A napból kialakult szivárvány a leggyakoribb. Az összes fajta közül a legfényesebb. Hét alapszínből áll: piros narancs, sárga, zöld, kék, indigó, ibolya. De ha a részleteket nézzük, sokkal több árnyalat létezik, mint amennyit a szemünk lát.
- A Hold által alkotott szivárvány éjszaka történik. Úgy tartják, hogy mindig látható. De a gyakorlat azt mutatja, hogy ez a jelenség alapvetően csak esős területeken vagy nagy vízesések közelében figyelhető meg. A holdi szivárvány színei nagyon homályosak. Csak speciális berendezések segítségével kell figyelembe venni őket. De még ezzel együtt is csak egy fehér csíkot tud kivenni a szemünk.
- A köd hatására megjelenő szivárvány olyan, mint egy széles, fénylő fényív. Néha ezt a típust összekeverik az előzővel. Felülről a színe lehet narancssárga, alulról lila árnyalatú. A ködön áthaladó napsugarak gyönyörű természeti jelenséget alkotnak.
- A tüzes szivárvány rendkívül ritka az égen. Vízszintes alakjában nem hasonlít az előző fajhoz. Ez a jelenség csak pehelyfelhők felett látható. Általában 8-10 kilométeres magasságban nyúlnak ki. Annak a szögnek, amelyben a szivárvány teljes pompájában megmutatkozik, 58 foknál nagyobbnak kell lennie. A színek általában ugyanazok maradnak, mint a szoláris szivárványban.
Golden Ratio (1, 618)
A tökéletes arány leggyakrabban az állatvilágban található. Olyan arányt kapnak, amely megegyezik a megfelelő számú PHI gyökérével. Ez az arány a bolygó összes állatának összekötő ténye. Az ókor nagy elméi ezt a számot isteni aránynak nevezték. Nevezhetjük aranymetszésnek is.
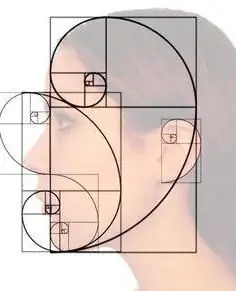
Ez a szabály teljes mértékben összhangban van az emberi szerkezet harmóniájával. Például, ha meghatározza a szem és a szemöldök közötti távolságot, akkor az egyenlő lesz az isteni állandóval.
Az aranymetszés jó példa arra, hogy a matematika mennyire fontos a természetben, melynek törvényét a tervezők, művészek, építészek, a szép és tökéletes dolgok megalkotói elkezdték követni. Az isteni állandó segítségével alkotják meg alkotásaikat, melyek kiegyensúlyozottak, harmonikusak és kellemes ránézésre. Az elménk tud számolniszépek azok a dolgok, tárgyak, jelenségek, ahol a részek egyenlőtlen aránya van. Az arányosság az, amit agyunk aranymetszésnek nevez.
DNS-spirál
Amint azt a német tudós, Hugo Weil helyesen megjegyezte, a szimmetria gyökerei a matematikán keresztül származnak. Sokan megjegyezték a geometriai alakzatok tökéletességét, és figyelmet fordítottak rájuk. Például a méhsejt nem más, mint egy hatszög, amelyet maga a természet hozott létre. Figyelni kell a lucfenyő kúpjaira is, amelyek hengeres alakúak. Ezenkívül gyakran előfordul egy spirál a külvilágban is: nagy és kis állatok szarvai, kagylóhéjak, DNS-molekulák.

A DNS-spirál az aranymetszés elve szerint jön létre. Ez egy kapocs az anyagi test séma és valós képe között. És ha az agyat vesszük, akkor az nem más, mint egy vezető a test és az elme között. Az értelem összekapcsolja az életet és annak megnyilvánulási formáját, és lehetővé teszi, hogy a formában lévő élet megismerje önmagát. Ennek segítségével az emberiség megértheti a környező bolygót, mintákat kereshet benne, amelyeket aztán a belső világ tanulmányozására alkalmaz.
Hasadás a természetben
A sejtmitózis négy fázisból áll:
- Profázis. Növeli a magot. Megjelennek a kromoszómák, amelyek spirálba kezdenek csavarodni, és szokásos formájukba fordulnak. Helyet alakítanak ki a sejtosztódásnak. A fázis végén a sejtmag és a membránja feloldódik, a kromoszómák a citoplazmába áramlanak. Ez a leghosszabb felosztási szakasz.
- Metafázis. Itt véget ér a kromoszómák spirálba csavarása, metafázis lemezt alkotnak. A kromatidák egymással szemben sorakoznak, felkészülve az osztódásra. Közöttük van egy hely a leválasztáshoz - egy orsó. Ezzel lezárult a második szakasz.
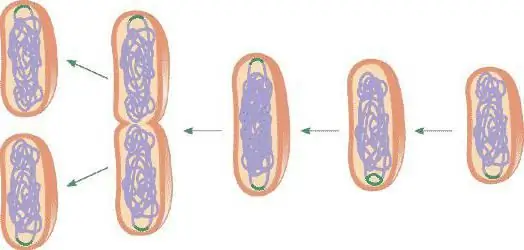
- Anafázis. A kromatidák ellentétes irányba mozognak. Most a sejtnek két kromoszómakészlete van osztódásuk miatt. Ez a szakasz nagyon rövid.
- Telofázis. A sejt minden felében egy-egy sejtmag képződik, amelyen belül kialakul a sejtmag. A citoplazma aktívan disszociál. Az orsó fokozatosan eltűnik.
A mitózis jelentése
Az egyedülálló osztódási módszernek köszönhetően a szaporodás után minden következő sejt ugyanolyan génösszetételű, mint az anyja. Mindkét sejt kromoszómáinak összetétele ugyanazt kapja. Nem nélkülözte az olyan tudományt, mint a geometria. A mitózis előrehaladása fontos, mivel minden sejt ennek az elvnek megfelelően szaporodik.
Honnan származnak a mutációk
Ez a folyamat garantálja a kromoszómák és a genetikai anyagok állandó készletét minden sejtben. A mitózis következtében a szervezet fejlődése, szaporodása, regenerációja következik be. Egyes mérgek hatására bekövetkező sejtosztódás megsértése esetén előfordulhat, hogy a kromoszómák nem oszlanak szét a felére, vagy szerkezeti zavarok léphetnek fel. Ez egyértelműen jelzi a kezdődő mutációkat.
Összegzés
Mi a közös a matematikában és a természetben? Cikkünkben megtalálja a választ erre a kérdésre. És ha mélyebbre ásol, szükséged lesz ráazt mondani, hogy a környező világ tanulmányozása segítségével az ember megismeri önmagát. A Legfelsőbb Elme nélkül, amely minden élőlényt szült, semmi sem történhetett volna. A természet kizárólag harmóniában van, törvényeinek szigorú sorrendjében. Lehetséges mindez ok nélkül?
Idézzük Henri Poincaré tudós, filozófus, matematikus és fizikus kijelentését, aki - mint senki más - meg tud majd válaszolni arra a kérdésre, hogy a matematika alapvető-e a természetben. Lehet, hogy egyes materialisták nem szeretik az ilyen érvelést, de nem valószínű, hogy meg tudják cáfolni. Poincaré szerint az a harmónia, amelyet az emberi elme fel akar fedezni a természetben, nem létezhet azon kívül. Az objektív valóság, amely legalább néhány egyén fejében jelen van, az egész emberiség számára elérhető. A szellemi tevékenységet összefogó kapcsolatot a világ harmóniájának nevezzük. Az utóbbi időben óriási előrelépés történt egy ilyen folyamat felé vezető úton, de ezek nagyon kicsik. Az Univerzumot és az egyént összekötő kapcsolatoknak értékesnek kell lenniük minden olyan emberi elme számára, amely érzékeny ezekre a folyamatokra.






