Vannak tárgyak, amelyek képesek megváltoztatni a rájuk eső elektromágneses sugárzási fluxus sűrűségét, vagyis vagy növelni egy ponton összegyűjtve, vagy csökkenteni szórással. Ezeket a tárgyakat a fizikában lencséknek nevezik. Nézzük meg közelebbről ezt a kérdést.
Mik azok a lencsék a fizikában?
Ez a fogalom abszolút minden olyan tárgyat jelent, amely képes megváltoztatni az elektromágneses sugárzás terjedési irányát. Ez a lencsék általános meghatározása a fizikában, amely magában foglalja az optikai szemüveget, a mágneses és a gravitációs lencséket.
Ebben a cikkben az optikai üvegeken lesz a hangsúly, amelyek átlátszó anyagból készült tárgyak, amelyeket két felület határol. Az egyik felületnek szükségszerűen görbülettel kell rendelkeznie (vagyis egy véges sugarú gömb része), különben az objektumnak nem lesz olyan tulajdonsága, hogy megváltoztatja a fénysugarak terjedési irányát.
Az objektív elve

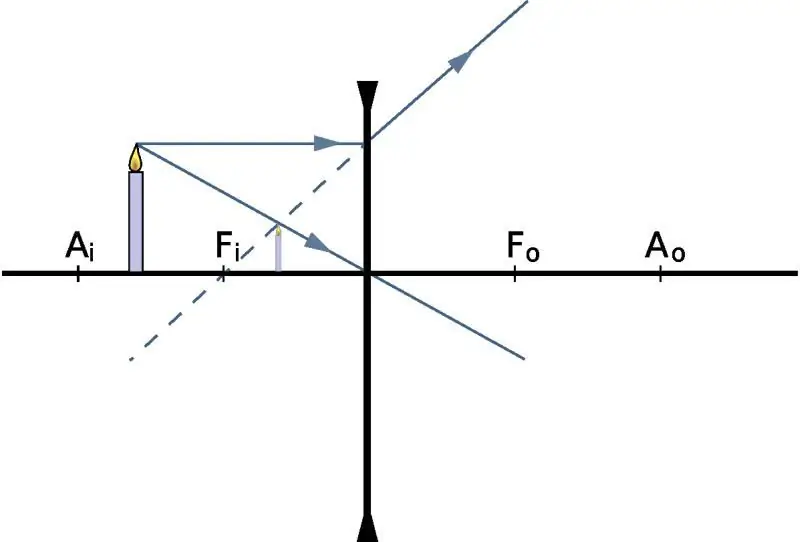
A munka lényege ennek az egyszerűnekaz optikai objektum a napsugarak törésének jelensége. A 17. század elején Willebrord Snell van Rooyen híres holland fizikus és csillagász kiadta a fénytörés törvényét, amely jelenleg az ő vezetéknevét viseli. Ennek a törvénynek a megfogalmazása a következő: amikor a napfény áthalad két optikailag átlátszó közeg határfelületén, akkor a nyaláb és a felület normálja közötti beesési szög szinuszának és a közeg törésmutatójának szorzata ez egy állandó érték.

A fentiek tisztázása érdekében mondjunk egy példát: a fény a víz felszínére hulljon, miközben a felszínhez viszonyított normál és a nyaláb közötti szög θ1. Ezután a fénysugár megtörik, és a vízben már a felszínhez képest θ2 szöget bezárva megkezdi a terjedését. Snell törvénye szerint a következőt kapjuk: sin(θ1)n1=sin(θ2) n2, ahol n1 és n2 a levegő és a víz törésmutatói, ill. Mi az a törésmutató? Ez az az érték, amely megmutatja, hogy az elektromágneses hullámok terjedési sebessége vákuumban hányszor nagyobb, mint egy optikailag átlátszó közegnél, azaz n=c/v, ahol c és v a fény sebessége vákuumban és közepes, illetve.
A fénytörés megjelenésének fizikája a Fermat-elv megvalósításában rejlik, amely szerint a fény úgy mozog, hogy a térben a legrövidebb idő alatt leküzdje a távolságot az egyik ponttól a másikig.
Lencsetípusok

Az optikai lencse típusát a fizikában kizárólag az azt alkotó felületek alakja határozza meg. A rájuk eső sugár törésiránya ettől az alaktól függ. Tehát, ha a felület görbülete pozitív (konvex), akkor a lencséből való kilépéskor a fénysugár közelebb fog terjedni az optikai tengelyéhez (lásd alább). Ezzel szemben, ha a felület görbülete negatív (konkáv), akkor az optikai üvegen áthaladva a sugár eltávolodik a központi tengelyétől.
Megjegyezzük meg még egyszer, hogy bármely görbületű felület ugyanúgy megtöri a sugarakat (a Stella törvénye szerint), de a hozzájuk tartozó normálok meredeksége eltérő az optikai tengelyhez képest, ami a megtört sugár eltérő viselkedését eredményezi.
A két konvex felület által határolt lencsét konvergáló lencsének nevezzük. Ha viszont két negatív görbületű felület alkotja, akkor szóródásnak nevezzük. Az összes többi optikai üvegtípus ezen felületek kombinációjához kapcsolódik, amelyhez egy sík is hozzáadódik. Az, hogy a kombinált lencse milyen tulajdonsággal rendelkezik (divergens vagy konvergens), a felületei sugarának teljes görbületétől függ.
Lencseelemek és sugártulajdonságok

A lencsék képfizikai beépítéséhez meg kell ismerkednie ennek az objektumnak az elemeivel. Az alábbiakban felsoroljuk őket:
- Fő optikai tengely és középpont. Az első esetben a lencsére merőlegesen áthaladó egyenest jelentik annak optikai középpontján. Ez utóbbi viszont egy pont a lencsén belül, amelyen áthaladva a sugár nem tapasztal törést.
- Fókusztávolság és fókusz - a középpont és az optikai tengely egy pontja közötti távolság, amely összegyűjti az objektívre e tengellyel párhuzamosan érkező összes sugarat. Ez a meghatározás igaz az optikai szemüvegek gyűjtésére. Divergens lencsék esetén nem maguk a sugarak fognak egy ponthoz konvergálni, hanem azok képzeletbeli folytatása. Ezt a pontot nevezzük fő fókusznak.
- Optikai teljesítmény. Ez a gyújtótávolság reciprokának neve, azaz D \u003d 1 / f. Dioptriában (dioptriában), azaz 1 dioptriában mérik.=1 m-1.
A lencsén áthaladó sugarak főbb tulajdonságai a következők:
- az optikai középponton áthaladó sugár nem változtatja meg mozgási irányát;
- a fő optikai tengellyel párhuzamosan beeső sugarak megváltoztatják irányukat, hogy áthaladjanak a fő fókuszon;
- az optikai üvegre tetszőleges szögben eső, de annak fókuszán áthaladó sugarak úgy változtatják terjedési irányukat, hogy párhuzamosak legyenek az optikai főtengellyel.
A sugarak fenti tulajdonságait a fizikában a vékony lencséknél (ahogy hívják, mert függetlenül attól, hogy milyen gömbök alkotják és milyen vastagságúak, csak a tárgy optikai tulajdonságai számítanak) képeket készítenek bennük..
Képek optikai szemüvegben: hogyan építsünk?
Az alábbi ábra részletezi a képek konvex és konkáv lencséiben történő létrehozásának sémáját(piros nyíl) a helyzetétől függően.
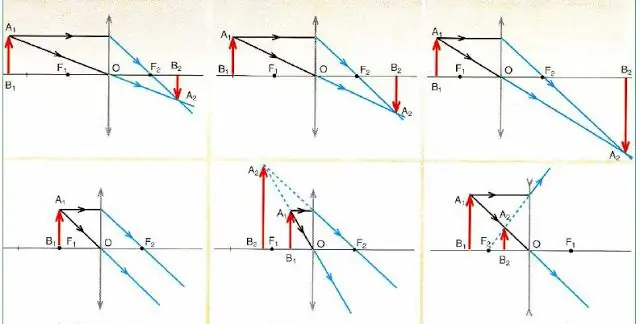
Fontos következtetések következnek az ábrán látható áramkörök elemzéséből:
- Bármely kép csak 2 sugárra épül (amely áthalad a középponton és párhuzamosan a fő optikai tengellyel).
- A konvergáló lencsék (a végén kifelé mutató nyilakkal jelölve) felnagyított és kicsinyített képet is adhatnak, ami viszont lehet valós (valós) vagy képzeletbeli.
- Ha a tárgy fókuszban van, akkor az objektív nem alkotja meg a képét (lásd az ábrán bal oldali alsó diagramot).
- A szétszórt optikai szemüvegek (amelyeket a végükön befelé mutató nyilak jelölnek) mindig kicsinyített és virtuális képet adnak, függetlenül az objektum helyzetétől.
A kép távolságának meghatározása
Annak meghatározásához, hogy milyen távolságban fog megjelenni a kép, ismerve magának a tárgynak a helyzetét, megadjuk a lencse képletét a fizikában: 1/f=1/do + 1 /d i, ahol do és di a távolság az objektumtól és a képtől az optikaitól középpontja, illetve f a fő fókusz. Ha gyűjtő optikai üvegről beszélünk, akkor az f-szám pozitív lesz. Ellenkezőleg, divergens objektív esetén f negatív.
Használjuk ezt a képletet, és oldjunk meg egy egyszerű feladatot: legyen a tárgy do=2f távolságra a gyűjtő optikai üveg középpontjától. Hol fog megjelenni a képe?
A probléma feltételéből a következőt kapjuk: 1/f=1/(2f)+1/di. Kezdő: 1/di=1/f - 1/(2f)=1/(2f), azaz di=2 f. Így a kép a lencsétől két fókusz távolságra, de a tárgy másik oldalán fog megjelenni (ezt a di érték pozitív előjele jelzi).
Egy rövid történelem
Kíváncsi lenne megadni a "lencse" szó etimológiáját. A latin lens és lentis szavakból származik, amelyek jelentése "lencse", mivel az optikai tárgyak formájukban valóban úgy néznek ki, mint ennek a növénynek a gyümölcse.
A gömb alakú átlátszó testek törőerejét az ókori rómaiak ismerték. Erre a célra vízzel töltött kerek üvegedényeket használtak. Magukat az üveglencséket csak a 13. században kezdték el készíteni Európában. Olvasóeszközként használták (modern szemüveg vagy nagyító).
Az optikai tárgyak aktív felhasználása teleszkópok és mikroszkópok gyártásában a 17. századra nyúlik vissza (e század elején Galilei találta fel az első távcsövet). Megjegyzendő, hogy a Stella-féle töréstörvény matematikai megfogalmazását, amelynek ismerete nélkül lehetetlen a kívánt tulajdonságokkal rendelkező lencséket előállítani, egy holland tudós tette közzé ugyanezen 17. század elején.
Egyéb objektívek
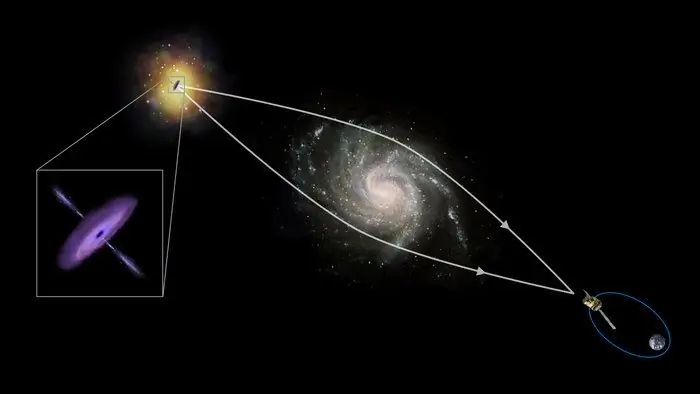
Amint fentebb említettük, az optikai fénytörő tárgyakon kívül vannak mágneses és gravitációs objektumok is. Előbbire példa a mágneses lencsék elektronmikroszkópban, az utóbbira pedig a fényáram irányának torzulása eleven példa,amikor hatalmas űrtestek (csillagok, bolygók) közelében halad el.






