A gáz hőkapacitása az az energiamennyiség, amelyet a test egy fokkal felmelegítve elnyel. Elemezzük ennek a fizikai mennyiségnek a főbb jellemzőit.

Definíciók
A gáz fajhője egy adott anyag egységnyi tömege. Mértékegységei: J/(kg·K). Az a hőmennyiség, amelyet a szervezet aggregációs állapotának megváltoztatása során felvesz, nemcsak a kezdeti és végső állapothoz, hanem az átmenet módjához is kapcsolódik.

Osztály
A gázok hőkapacitását elosztjuk az állandó térfogaton (Cv), állandó nyomáson (Cр) meghatározott értékkel.
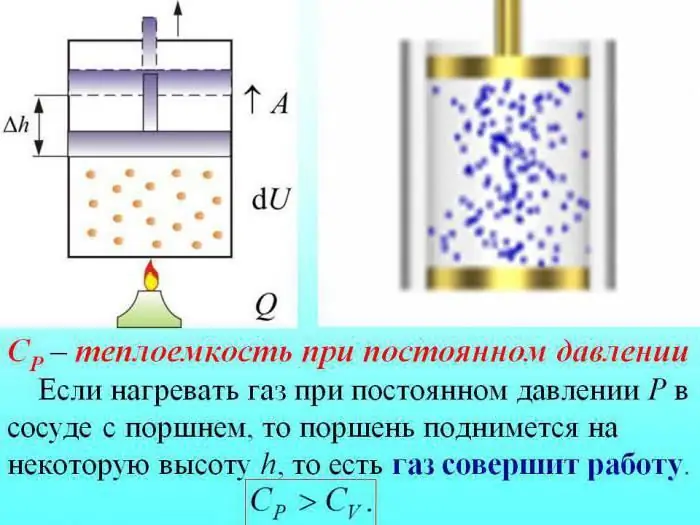
Nyomásváltoztatás nélküli fűtés esetén a hő egy részét a gáztágulási munkára, az energia egy részét pedig a belső energia növelésére fordítják.
A gázok állandó nyomású hőkapacitását a belső energia növelésére fordított hőmennyiség határozza meg.
Gázállapot: jellemzők, leírás
Az ideális gáz hőkapacitását annak figyelembevételével határozzuk meg, hogy Сp-Сv=R. Ez utóbbi mennyiséget univerzális gázállandónak nevezzük. Értéke 8,314 J/(mol K).
A hőkapacitás elméleti számításainál, például a hőmérséklettel való kapcsolat leírásánál nem elég csak termodinamikai módszereket alkalmazni, fontos a statikus fizika elemeivel is felvértezni.
A gázok hőkapacitása magában foglalja egyes molekulák transzlációs mozgásának energiájának átlagértékének kiszámítását. Ezt a mozgást a molekula forgó és transzlációs mozgása, valamint az atomok belső rezgései összegzik.
A statikus fizikában vannak olyan információk, amelyek szerint a forgó és transzlációs mozgás szabadságának minden fokára van egy gázmennyiség, amely egyenlő az univerzális gázállandó felével.

Érdekes tények
Feltételezzük, hogy egy monoatomos gáz részecskéjének három transzlációs szabadságfoka van, így a gáz fajhője három transzlációs, két forgási és egy rezgési szabadságfokkal rendelkezik. Egyenletes eloszlásuk törvénye azt eredményezi, hogy az állandó térfogatú fajhőt R.
A kísérletek során kiderült, hogy a kétatomos gáz hőkapacitása megfelel az R értéknek. Az elmélet és a gyakorlat közötti ilyen eltérést az magyarázza, hogy az ideális gáz hőkapacitása kvantumhoz kapcsolódik. hatások, ezért a számítások elvégzésekor fontos a kvantum alapú statisztikák használatamechanika.
A kvantummechanika alapjai alapján minden oszcilláló vagy forgó részecskerendszer, beleértve a gázmolekulákat is, csak néhány diszkrét energiaértékkel rendelkezik.
Ha a rendszerben a hőmozgás energiája nem elegendő egy bizonyos frekvenciájú rezgések gerjesztéséhez, az ilyen mozgások nem járulnak hozzá a rendszer teljes hőkapacitásához.
Ennek eredményeként a szabadság bizonyos foka „befagy”, nem lehet rá alkalmazni az egyenlőség törvényét.
A gázok hőkapacitása fontos jellemzője annak az állapotnak, amelytől a teljes termodinamikai rendszer működése függ.
Azt a hőmérsékletet, amelyen az egyenlítés törvénye alkalmazható a rezgési vagy forgási szabadságfokra, a kvantumelmélet jellemzi, amely összekapcsolja a Planck-állandót a Boltzmann-állandóval.

Kétatomos gázok
Az ilyen gázok forgási energiaszintjei közötti hézagok kis számú fok. Kivétel a hidrogén, amelyben a hőmérséklet értékét több száz fok határozza meg.
Ezért egy gáz állandó nyomású hőkapacitása nehezen írható le az egyenletes eloszlás törvényével. A kvantumstatisztikában a hőkapacitás meghatározásakor figyelembe veszik, hogy annak rezgési része a hőmérséklet csökkenése esetén gyorsan lecsökken és eléri a nullát.
Ez a jelenség magyarázza azt a tényt, hogy szobahőmérsékleten gyakorlatilag nincs rezgési része a hőkapacitásnak, pl.kétatomos gáz, az R állandónak felel meg.
A gáz állandó térfogatú hőkapacitását alacsony hőmérsékletű indikátorok esetén kvantumstatisztika segítségével határozzuk meg. Létezik a Nernst-elv, amelyet a termodinamika harmadik főtételének neveznek. Összetétele alapján a gáz moláris hőkapacitása a hőmérséklet csökkenésével csökken, és nullára hajlik.

Szilárd testek jellemzői
Ha a gázkeverék hőkapacitása kvantumstatisztika segítségével magyarázható, akkor szilárd halmazállapotú aggregáció esetén a hőmozgást a részecskék enyhe ingadozása jellemzi az egyensúlyi helyzet közelében.
Minden atomnak három rezgési szabadsági foka van, ezért az ekvipartíciós törvény értelmében a szilárd test moláris hőkapacitása 3nR-ként számítható, ahol n a molekulában lévő atomok száma.
A gyakorlatban ez a szám az a határ, amelyre a szilárd test hőkapacitása magas hőmérsékleten hajlik.
Egyes elemek, köztük a fémek esetében a maximum normál hőmérsékleten érhető el. N=1 esetén a Dulong- és Petit-törvény teljesül, de összetett anyagoknál meglehetősen nehéz ezt a határt elérni. Mivel a határértéket a valóságban nem lehet megadni, a szilárd anyag bomlása vagy megolvadása következik be.
A kvantumelmélet története
A kvantumelmélet megalapítói Einstein és Debye a huszadik század elején. Az atomok rezgőmozgásának kvantálásán alapul egy bizonyoskristály. Alacsony hőmérsékleti mutatók esetén a szilárd test hőkapacitása egyenesen arányos a kockára vett abszolút értékkel. Ezt a kapcsolatot Debye törvényének nevezték. Kritériumként, amely lehetővé teszi az alacsony és a magas hőmérsékletű indikátorok megkülönböztetését, a Debye hőmérséklettel való összehasonlításukat veszik figyelembe.
Ezt az értéket a testben lévő atom rezgési spektruma határozza meg, ezért komolyan függ a kristályszerkezetének jellemzőitől.
A
QD olyan érték, amely több száz K-t tartalmaz, de például gyémántban sokkal magasabb.
A vezetési elektronok jelentősen hozzájárulnak a fémek hőkapacitásához. Kiszámításához a Fermi kvantumstatisztikát használjuk. A fématomok elektronikus vezetőképessége egyenesen arányos az abszolút hőmérséklettel. Mivel ez jelentéktelen érték, csak az abszolút nulla felé hajló hőmérsékleten veszik figyelembe.
A hőkapacitás meghatározásának módszerei
A fő kísérleti módszer a kalorimetria. A hőkapacitás elméleti számításának elvégzéséhez statisztikai termodinamikát használnak. Ideális gázra, valamint kristályos testekre érvényes, az anyag szerkezetére vonatkozó kísérleti adatok alapján végezzük.
Az ideális gáz hőkapacitásának kiszámítására szolgáló empirikus módszerek a kémiai szerkezet elgondolásán, az egyes atomcsoportok hozzájárulásán alapulnak a Ср.
A folyadékok esetében olyan módszereket is alkalmaznak, amelyek a termodinamika használatán alapulnakciklusok, amelyek lehetővé teszik az ideális gáz hőkapacitásából a folyadékba való átmenetet a párolgási folyamat entalpiájának hőmérsékletének deriváltja révén.
Megoldás esetén a hőkapacitás számítása additív függvényként nem megengedett, mivel az oldat hőkapacitásának többletértéke alapvetően jelentős.
A kiértékeléséhez szükségünk van a megoldások molekuláris-statisztikai elméletére. A legnehezebb a heterogén rendszerek hőkapacitásának azonosítása termodinamikai elemzésben.

Következtetés
A hőkapacitás vizsgálata lehetővé teszi a vegyi reaktorokban, valamint más vegyszergyártó berendezésekben lezajló folyamatok energiamérlegének kiszámítását. Ezenkívül ez az érték szükséges a hűtőfolyadékok optimális típusának kiválasztásához.
Jelenleg az anyagok hőkapacitásának kísérleti meghatározása különböző hőmérsékleti intervallumokban - az alacsony értékektől a magas értékekig - a fő lehetőség egy anyag termodinamikai jellemzőinek meghatározására. Egy anyag entrópiájának és entalpiájának számításakor hőkapacitási integrálokat használunk. A kémiai reagensek hőkapacitásával kapcsolatos információk egy bizonyos hőmérsékleti tartományban lehetővé teszik a folyamat termikus hatásának kiszámítását. Az oldatok hőkapacitására vonatkozó információk lehetővé teszik termodinamikai paramétereik kiszámítását bármely hőmérsékleti értéknél az elemzett intervallumon belül.
Például egy folyadékot az jellemez, hogy a hő egy részét a potenciális energia értékének megváltoztatására fordítja.reagáló molekulák. Ezt az értéket "konfigurációs" hőkapacitásnak nevezik, és a megoldások leírására szolgál.
Nehéz teljes értékű matematikai számításokat végezni anélkül, hogy figyelembe vennénk egy anyag termodinamikai jellemzőit, aggregáltsági állapotát. Ezért a folyadékok, gázok, szilárd anyagok esetében olyan jellemzőt használnak, mint a fajlagos hőkapacitás, amely lehetővé teszi az anyag energiaparamétereinek jellemzését.






