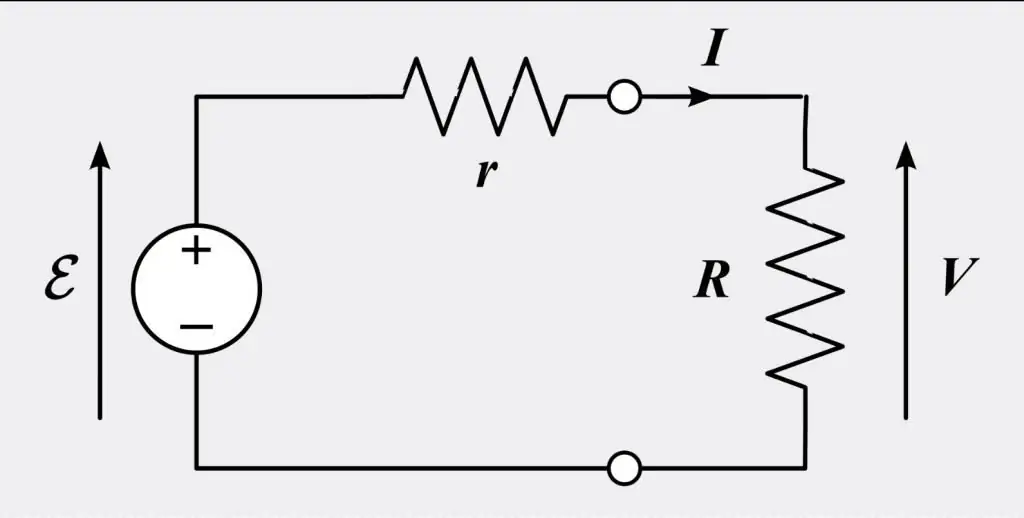
Ohm törvénye differenciális és integrál formában kimondja, hogy a két pont közötti vezetőn áthaladó áram egyenesen arányos a két pont feszültségével. Egy konstans egyenlet így néz ki:
I=V/R, ahol I a vezetőn áthaladó áram pontja amper egységekben, V (Volt) a vezetővel mért feszültség volt egységekben, R pedig az átvezetett anyag ellenállása ohmban. Pontosabban, Ohm törvénye kimondja, hogy R ebben a tekintetben állandó, független az áramerősségtől.
Mit érthetünk az "Ohm-törvényen"?
Az Ohm-törvény differenciális és integrál formában egy empirikus összefüggés, amely pontosan leírja a vezető anyagok túlnyomó többségének vezetőképességét. Egyes anyagok azonban nem engedelmeskednek Ohm törvényének, ezeket "nemohmikusnak" nevezik. A törvényt Georg Ohm tudósról nevezték el, aki 1827-ben publikálta. Feszültség- és áramméréseket ír le egyszerű elektromos áramkörök segítségével, amelyek tartalmazzákkülönféle huzalhosszúságok. Ohm kísérleti eredményeit a fenti modern formánál valamivel összetettebb egyenlettel magyarázta.
Az Ohm-törvény fogalma a diff. A formát különféle általánosítások jelölésére is használják, például vektoros alakját használják az elektromágnesességben és az anyagtudományban:
J=σE, ahol J az elektromos részecskék száma az ellenálló anyag egy adott helyén, e az elektromos tér ezen a helyen, és σ (szigma) a vezetőképességi paramétertől függő anyag. Gustav Kirchhoff pontosan így fogalmazta meg a törvényt.
Előzmények

Előzmények
1781 januárjában Henry Cavendish egy Leyden-edényt és egy különféle átmérőjű, sóoldattal megtöltött üvegcsővel kísérletezett. Cavendish azt írta, hogy a sebesség közvetlenül változik a villamosítás mértékével. Kezdetben az eredmények ismeretlenek voltak a tudományos közösség számára. De Maxwell 1879-ben publikálta őket.
Ohm 1825-ben és 1826-ban végezte az ellenállással kapcsolatos munkáját, eredményeit pedig 1827-ben publikálta a "The Galvanic Circuit Proved Mathematically" c. Fourier francia matematikus munkája ihlette meg, aki a hővezetést írta le. A kísérletekhez kezdetben galvanikus cölöpöket használt, később azonban hőelemekre tért át, amelyek stabilabb feszültségforrást tudtak biztosítani. A belső ellenállás és az állandó feszültség fogalmával operált.
Ezekben a kísérletekben is galvanométert használtak az áram mérésére, mivel a feszültséga hőelem kivezetései között a csatlakozási hőmérséklettel arányos. Ezután különféle hosszúságú, átmérőjű és anyagú mérővezetékeket adott hozzá az áramkör teljessé tételéhez. Úgy találta, hogy adatai modellezhetők a következő egyenlettel:
x=a /b + l, ahol x a mérőállás, l a mérővezeték hossza, a a hőelem csatlakozásának hőmérsékletétől függ, b a teljes egyenlet állandója (állandója). Ohm ezen arányossági számítások alapján bizonyította törvényét, és közzétette eredményeit.
Ohm törvényének jelentősége
Az Ohm-törvény differenciális és integrál alakban valószínűleg a legfontosabb volt az elektromosság fizikájának korai leírásai közül. Ma ezt szinte magától értetődőnek tartjuk, de amikor Om először publikálta munkáját, nem ez volt a helyzet. A kritikusok ellenségesen reagáltak értelmezésére. Munkáját "meztelen fantáziának" nevezték, a német oktatási miniszter pedig kijelentette, hogy "az a professzor, aki ilyen eretnekséget hirdet, méltatlan arra, hogy tudományt tanítson."
A Németországban akkoriban uralkodó tudományos filozófia azt tartotta, hogy a természet megértéséhez nincs szükség kísérletekre. Ráadásul Geogr bátyja, Martin, hivatása szerint matematikus, a német oktatási rendszerrel küszködött. Ezek a tényezők megakadályozták Ohm munkájának elfogadását, és munkája csak az 1840-es években vált széles körben elfogadottá. Ennek ellenére Om már jóval halála előtt elismerést kapott a tudományhoz való hozzájárulásáért.
Az Ohm törvénye differenciális és integrál formában egy empirikus törvény,számos kísérlet eredményeinek általánosítása, amelyek azt mutatták, hogy az áramerősség a legtöbb anyag esetében megközelítőleg arányos az elektromos térfeszültséggel. Ez kevésbé alapvető, mint a Maxwell-egyenletek, és nem alkalmas minden helyzetben. Bármely anyag lebomlik elegendő elektromos tér hatására.
Az Ohm törvényét sokféle skálán megfigyelték. A 20. század elején az Ohm-törvényt nem tekintették atomi léptékben, de a kísérletek ennek az ellenkezőjét igazolják.
Kvantumkezdet
Az áramsűrűség függése az alkalmazott elektromos tértől alapvetően kvantummechanikai jellegű (klasszikus kvantumpermeabilitás). Az Ohm-törvény kvalitatív leírása a klasszikus mechanikán alapulhat, a Paul Drude német fizikus által 1900-ban kidolgozott Drude-modell segítségével. Emiatt az Ohm-törvénynek számos formája van, például az úgynevezett differenciális Ohm-törvény.
Az Ohm-törvény egyéb formái
Az Ohm-törvény differenciál formában rendkívül fontos fogalom az elektromos/elektronikai mérnökökben, mert mind a feszültséget, mind az ellenállást leírja. Mindez makroszkopikus szinten összefügg. Az elektromos tulajdonságok makro- vagy mikroszkopikus szintű tanulmányozásakor egy rokonabb egyenletet használnak, amelyet "Ohm-egyenletnek" nevezhetünk, és amelynek változói szorosan kapcsolódnak az Ohm-törvény V, I és R skaláris változóihoz, de pozíciójának állandó függvényefelfedező.
A mágnesesség hatása

Ha külső mágneses tér (B) van jelen, és a vezető nincs nyugalomban, hanem V sebességgel mozog, akkor egy további változót kell hozzáadni a töltésre ható Lorentz-erő által indukált áram figyelembevételéhez. szállítók. Az integrál alak Ohm-törvényének is nevezik:
J=σ (E + vB).
A mozgó vezető nyugalmi keretében ez a kifejezés kimarad, mert V=0. Nincs ellenállás, mert a nyugalmi keret elektromos mezője eltér a laboratóriumi keretben lévő E-tértől: E'=E + v × B. Az elektromos és a mágneses tér relatív. Ha J (áram) változó, mert az alkalmazott feszültség vagy E-mező idővel változik, akkor a reaktanciát hozzá kell adni az ellenálláshoz, hogy figyelembe vegyék az önindukciót. A reaktancia erős lehet, ha a frekvencia magas, vagy a vezető fel van tekercselve.






