A gyorsulás és a sebesség bármely mozgástípus két fontos kinematikai jellemzője. Ezeknek a mennyiségeknek az időtől való függésének ismerete lehetővé teszi a test által megtett út kiszámítását. Ebben a cikkben megtaláljuk a választ arra a kérdésre, hogy hogyan lehet megtalálni a gyorsulást a sebesség és az idő ismeretében.
A sebesség és a gyorsulás fogalma
Mielőtt választ adnánk arra a kérdésre, hogy a sebesség és az idő ismeretében hogyan találjuk meg a gyorsulást, vegyük figyelembe az egyes jellemzőket a fizika szempontjából.
A sebesség egy olyan érték, amely meghatározza a koordináták térbeli változásának sebességét, amikor a test mozog. A sebesség kiszámítása a következő képlettel történik:
v=dl/dt.
Ahol dl a test által a dt idő alatt megtett út. A sebesség mindig a mozgási útvonal érintője mentén irányul.
A mozgás történhet időben állandó sebességgel vagy változó sebességgel. Ez utóbbi esetben a gyorsulás jelenlétéről beszélünk. A fizikában a gyorsulás határozza meg v változásának sebességét, amelyet képletként írunk fel:
a=dv/dt.
Ez az egyenlőség a válasz arra a kérdésre, hogy hogyan lehet megtalálnisebesség gyorsulás. Ehhez elég csak a v.
első deriváltját venni
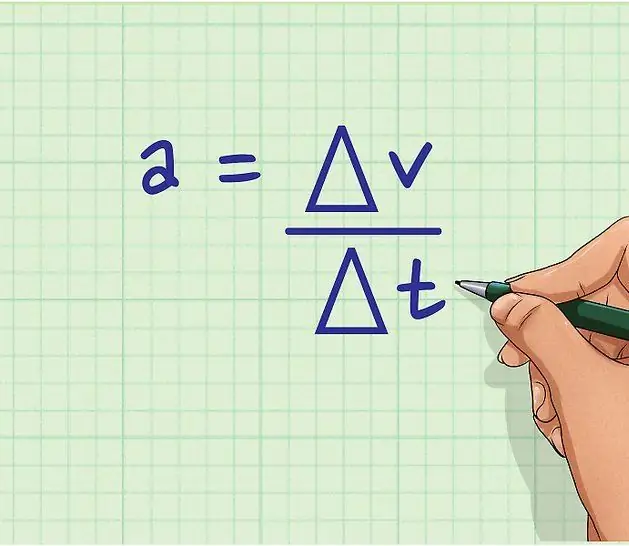
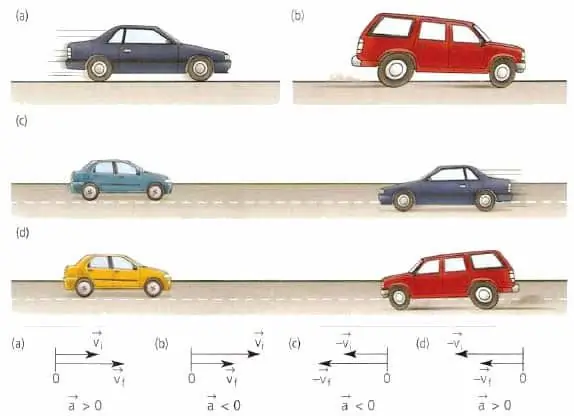
A gyorsulás iránya egybeesik a sebességvektorok különbségének irányával. Egyenes irányú gyorsított mozgás esetén az a és v mennyiségek egy irányba irányulnak.
Hogyan lehet megtalálni a gyorsulást adott sebesség és idő függvényében?
A mechanika tanulmányozása során először az egyenletes és egyenletesen gyorsított mozgástípusokat vesszük figyelembe az egyenes pálya mentén. Mindkét esetben a Δt időintervallumot kell választani a gyorsulás meghatározásához. Ezután meg kell határozni a v1 és v2 sebességek értékeit ennek az intervallumnak a végén. Az átlagos gyorsulás meghatározása a következő:
a=(v2- v1)/Δt.
Egyenletes mozgás esetén a sebesség állandó marad (v2=v1), tehát az akarat értéke legyen nulla. Egyenletesen gyorsuló mozgás esetén az a érték állandó lesz, tehát nem függ a képletben szereplő Δt időintervallumtól.
A mozgás bonyolultabb eseteinél, amikor a sebesség az idő függvénye, az a-n át a derivált képletet kell használnia, amelyet a fenti bekezdésben mutattunk be.
Példa problémamegoldásra
A gyorsulás megtalálásának kérdésével foglalkozva, az idő és a sebesség ismeretében megoldunk egy egyszerű problémát. Tegyük fel, hogy a test egy bizonyos pályán haladva megváltoztatja a sebességét a következő egyenlet szerint:
v=3t2- t + 4.
Mekkora lesz a test gyorsulása t=5 másodpercnél?
A gyorsulás v első deriváltja a t változóhoz viszonyítva, a következőket kapjuk:
a=dv/dt=6t - 1.
A probléma kérdésének megválaszolásához be kell cserélnie az idő ismert értékét a kapott egyenletbe: a=29 m/c2.






