A statisztikai rendszerekben lezajló folyamatok tanulmányozását nehezíti a részecskék minimális mérete és óriási száma. Gyakorlatilag lehetetlen minden részecskét külön-külön megvizsgálni, ezért statisztikai mennyiségeket vezetünk be: a részecskék átlagos sebességét, koncentrációját, részecsketömeget. A rendszer állapotát a mikroszkopikus paraméterek figyelembevételével jellemző képletet a gázok molekuláris-kinetikai elméletének (MKT) alapegyenletének nevezzük.
Egy kicsit az átlagos részecskesebességről
A részecskék sebességének meghatározását először kísérletileg végezték el. Az iskolai tantervből jól ismert kísérlet, amelyet Otto Stern végzett, lehetővé tette a részecskesebességről alkotott elképzelést. A kísérlet során az ezüstatomok mozgását vizsgálták forgó hengerekben: először a berendezés álló állapotában, majd bizonyos szögsebességgel forogva.
Ennek eredményeként azt találták, hogy az ezüstmolekulák sebessége meghaladja a hangsebességet, és 500 m/s. A tény meglehetősen érdekes, mivel az ember nehezen érzékeli a részecskék ilyen sebességét az anyagokban.
Ideális gáz
Folytasd a kutatástEz csak olyan rendszerben tűnik lehetségesnek, amelynek paraméterei fizikai műszerekkel történő közvetlen méréssel meghatározhatók. A sebességet sebességmérővel mérik, de a sebességmérő egyetlen részecskére történő rögzítése abszurd. Csak a részecske mozgásához kapcsolódó makroszkopikus paraméter mérhető közvetlenül.
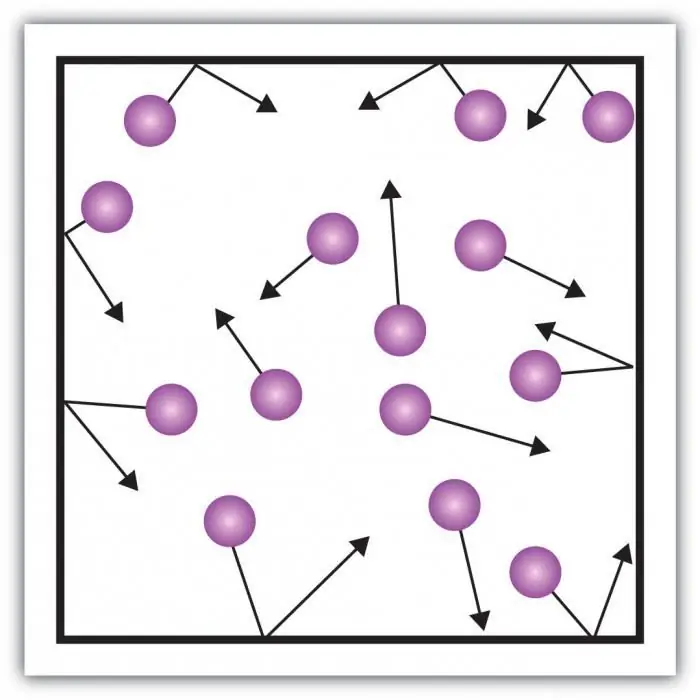
Vegye figyelembe a gáznyomást. Az edény falára nehezedő nyomást az edényben lévő gázmolekulák becsapódása hozza létre. Az anyag gázhalmazállapotának sajátossága a részecskék közötti kellően nagy távolságokban és kis kölcsönhatásban rejlik egymással. Ez lehetővé teszi a nyomás közvetlen mérését.
A kölcsönható testek bármely rendszerét a potenciális energia és a mozgás kinetikus energiája jellemez. A valódi gáz összetett rendszer. A potenciális energia változékonysága nem alkalmas rendszerezésre. A probléma megoldható egy olyan modell bevezetésével, amely a gáz jellemző tulajdonságait hordozza, félresöpörve a kölcsönhatás bonyolultságát.
Az ideális gáz olyan halmazállapot, amelyben a részecskék kölcsönhatása elhanyagolható, a kölcsönhatás potenciális energiája nullára hajlik. Csak a mozgás energiája tekinthető jelentősnek, amely a részecskék sebességétől függ.
Ideális gáznyomás
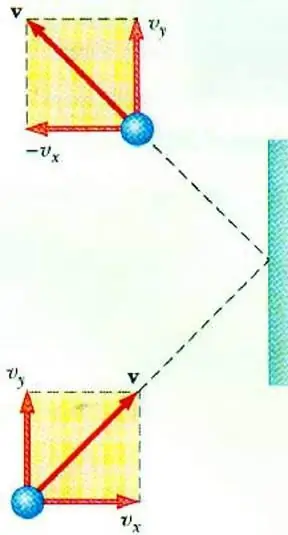
A gáznyomás és a részecskék sebessége közötti kapcsolat feltárása lehetővé teszi az ideális gáz MKT-jának alapegyenletét. Az edényben mozgó részecske a falnak ütközve impulzust ad át neki, melynek értéke a második törvény alapján határozható meg. Newton:
F∆t=2m0vx
Egy részecske lendületének változása a rugalmas ütközés során a sebesség vízszintes komponensének megváltozásával jár. F a részecske oldaláról a falra ható erő rövid ideig t; m0 - részecsketömeg.
Minden gázrészecske ütközik az S terület felületével ∆t idő alatt, vx sebességgel haladva a felület irányába, és egy Sυ térfogatú hengerben helyezkedik el. x Δt. Az n részecskekoncentrációnál a molekulák pontosan a fele a fal felé, a másik fele az ellenkező irányba mozog.
Az összes részecske ütközését figyelembe véve felírhatjuk Newton törvényét a területre ható erőre:
F∆t=nm0vx2S∆t
Mivel a gáznyomást a felületre merőlegesen ható erőnek az utóbbi területéhez viszonyított arányaként definiáljuk, ezt írhatjuk:
p=F: S=nm0vx2
A kapott reláció, mint az MKT alapegyenlete, nem írja le a teljes rendszert, mivel csak egy mozgásirányt veszünk figyelembe.
Maxwell disztribúció
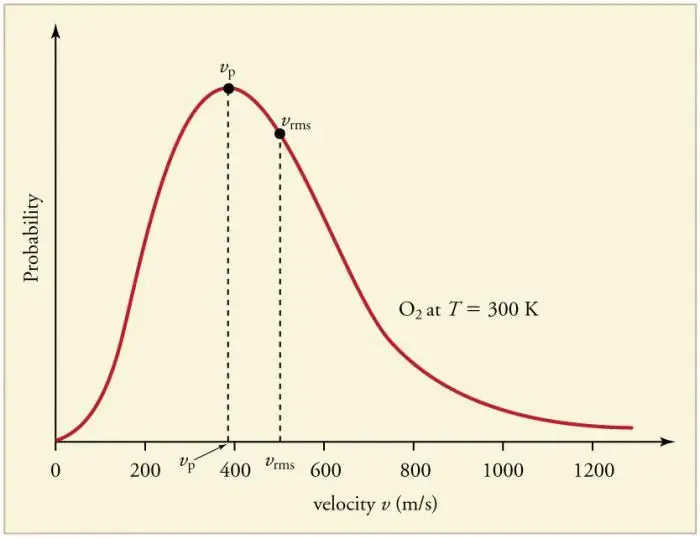
A gázrészecskék falakkal és egymással való folyamatos, gyakori ütközései a részecskék bizonyos statisztikai eloszlásának megállapításához vezetnek a sebességek (energiák) tekintetében. Minden sebességvektor iránya egyformán valószínű. Ezt az eloszlást Maxwell-eloszlásnak nevezik. 1860-ban ez a minta voltJ. Maxwell származtatta az MKT alapján. Az eloszlási törvény főbb paramétereit sebességeknek nevezzük: valószínű, a görbe maximális értékének megfelelő, és a négyzetgyökér vkv=√‹v2 › - a részecskesebesség középnégyzete.
A gáz hőmérsékletének növekedése a sebesség növekedésének felel meg.
Annak alapján, hogy minden sebesség egyenlő, és a moduljaik azonos értékűek, feltételezhetjük:
‹v2›=‹vx2› + ‹v y2› + ‹vz2›, innen: ‹ vx2›=‹v2›: 3
Az MKT alapegyenlete a gáznyomás átlagértékét figyelembe véve a következő:
p=nm0‹v2›: 3.
Ez az összefüggés abban egyedülálló, hogy meghatározza a mikroszkopikus paraméterek közötti kapcsolatot: sebesség, részecsketömeg, részecskekoncentráció és általában a gáznyomás.
A részecskék kinetikus energiájának fogalmát használva az MKT alapegyenlete másképp is átírható:
p=2nm0‹v2›: 6=2n‹Ek›: 3
Egy gáz nyomása arányos részecskéi kinetikus energiájának átlagos értékével.
Hőmérséklet
Érdekes, hogy egy zárt edényben állandó gázmennyiség esetén összefüggésbe hozható a gáznyomás és a részecske mozgási energiájának átlagos értéke. Ebben az esetben a nyomást az energia mérésével lehet mérnirészecskék.
Mit tegyek? Milyen értéket lehet összehasonlítani a mozgási energiával? A hőmérséklet ilyen értéknek bizonyul.

A hőmérséklet az anyagok termikus állapotának mértéke. Méréséhez hőmérőt használnak, melynek alapja a munkafolyadék (alkohol, higany) hőtágulása hevítéskor. A hőmérő skála kísérleti úton készül. Általában valamilyen állandó termikus állapotban végbemenő fizikai folyamat során (forrásban lévő víz, olvadó jég) a munkaközeg helyzetének megfelelő jeleket helyeznek el rajta. A különböző hőmérőknek különböző skálája van. Például Celsius, Fahrenheit.

Univerzális hőmérsékleti skála
A gázhőmérők érdekesebbnek tekinthetők a munkaközeg tulajdonságaitól való függetlenség szempontjából. Mértékük nem függ a használt gáz típusától. Egy ilyen készülékben hipotetikusan ki lehet választani azt a hőmérsékletet, amelyen a gáznyomás nullára hajlik. A számítások azt mutatják, hogy ez az érték -273,15 oC-nak felel meg. A hőmérsékleti skálát (abszolút hőmérsékleti skála vagy Kelvin-skála) 1848-ban vezették be. A skála fő pontjának a nulla gáznyomás lehetséges hőmérsékletét vettük. A skála egységnyi szegmense megegyezik a Celsius-skála egységértékével. Kényelmesebbnek tűnik az alapvető MKT egyenletet a hőmérséklet segítségével felírni a gázfolyamatok tanulmányozásakor.
A nyomás és a hőmérséklet kapcsolata
Tempirikusan ezt ellenőrizhetia gáznyomás és a hőmérséklet arányossága. Ugyanakkor azt találták, hogy a nyomás egyenesen arányos a részecskék koncentrációjával:
P=nkT,
ahol T az abszolút hőmérséklet, k egy állandó, egyenlő 1,38•10-23J/K.
Az alapértéket, amelynek minden gázra állandó értéke van, Boltzmann-állandónak nevezzük.
A nyomás hőmérséklettől való függését és az MKT gázok alapegyenletét összehasonlítva felírhatjuk:
‹Ek›=3kT: 2
A gázmolekulák mozgásának kinetikus energiájának átlagos értéke arányos a hőmérsékletével. Vagyis a hőmérséklet a részecskék mozgásának kinetikus energiájának mértékeként szolgálhat.

