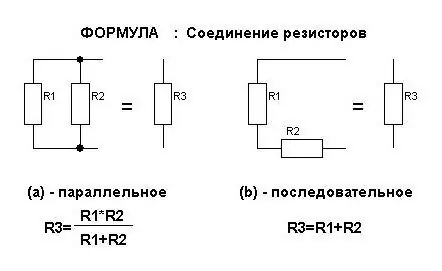
A fizikában a párhuzamos és soros kapcsolás témakörét tanulmányozzák, és ez lehet nem csak vezető, hanem kondenzátor is. Itt fontos, hogy ne keveredjen bele abba, hogy mindegyik hogyan néz ki a diagramon. És csak ezután alkalmazzon speciális képleteket. Mellesleg fejből kell emlékezned rájuk.
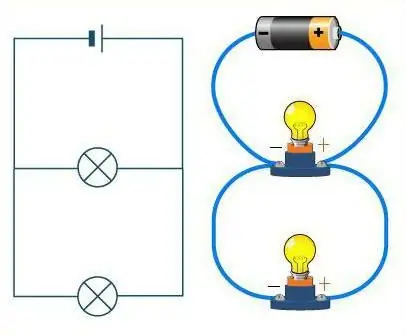
Hogyan lehet megkülönböztetni ezt a két vegyületet?
Nézze meg alaposan az ábrát. Ha a vezetékek útként vannak ábrázolva, akkor a rajta lévő autók ellenállások szerepét töltik be. Egyenes úton minden elágazás nélkül egymás után, láncban haladnak az autók. Ugyanígy néz ki a vezetékek soros csatlakozása is. Az út ebben az esetben korlátlan számú kanyarral rendelkezhet, de egyetlen kereszteződés sem. Nem számít, hogy az út (vezetékek) milyen hullámzóan mozog, a gépek (ellenállások) mindig egymás után, egy láncban helyezkednek el.
Az egészen más kérdés, ha párhuzamos kapcsolatot vesszük figyelembe. Ezután az ellenállások összehasonlíthatók a sportolókkal az elején. Őkmindegyik a saját pályáján áll, de ugyanaz a mozgási irányuk, és a célvonal ugyanazon a helyen van. Hasonlóképpen az ellenállások is - mindegyiknek megvan a maga vezetéke, de mindegyik egy ponton össze van kötve.
A jelenlegi erősség képlete
Mindig az "Villany" témakörben lesz szó róla. A párhuzamos és soros csatlakozások különböző módon befolyásolják az ellenállások áramerősségét. Számukra képletek származnak, amelyek megjegyezhetők. De elég csak emlékezni a beléjük fektetett jelentésre.
Tehát a vezetékek soros bekötésének árama mindig ugyanaz. Vagyis mindegyikben nem különbözik az áramerősség értéke. Hasonlítást vonhat le, ha összehasonlít egy vezetéket egy csővel. Ebben mindig ugyanúgy folyik a víz. És az útjába kerülő összes akadályt ugyanolyan erővel sodorják el. Ugyanez az árammal. Ezért az ellenállások soros csatlakoztatásával rendelkező áramkör teljes áramának képlete így néz ki:
I gen=I 1=I 2
Itt az I betű az áramerősséget jelöli. Ez egy általános jelölés, ezért emlékeznie kell rá.
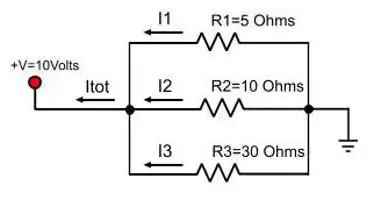
A párhuzamosan kapcsolt áram már nem lesz állandó érték. A csővel azonos analógia alapján kiderül, hogy a víz két patakra oszlik, ha a főcsőnek van egy ága. Ugyanez a jelenség figyelhető meg az áramnál, amikor vezetékek elágazása jelenik meg az útjában. A teljes áramerősség képlete, amikor a vezetékek párhuzamosan vannak csatlakoztatva:
I gen=I 1 + I 2
Ha az elágazás olyan vezetékekből áll, amelyekkettőnél több, akkor a fenti képletben több tag lesz azonos számmal.
Stresszképletek
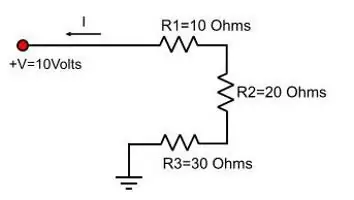
Ha egy olyan áramkört veszünk figyelembe, amelyben a vezetők sorba vannak kötve, a feszültséget a teljes szakaszban ezen értékek összege határozza meg az egyes ellenállásokon. Ezt a helyzetet összehasonlíthatja a lemezekkel. Egy embernek könnyű lesz megfognia az egyiket, a másodikat is el tudja venni a közelben, de nehezen. Egy ember már nem tud három tányért egymás mellé tartani, egy második segítségére lesz szükség. Stb. Az emberek erőfeszítései összeadódnak.
Az áramkör egy szakaszának teljes feszültségének képlete a vezetékek soros csatlakoztatásával a következőképpen néz ki:
U gen=U 1 + U 2, ahol U az elfogadott jelölés elektromos feszültségre.
Másik helyzet adódik, ha az ellenállások párhuzamos csatlakoztatását vesszük figyelembe. Ha a tányérokat egymásra rakják, egy személy továbbra is megtarthatja őket. Tehát nem kell hozzátenned semmit. Ugyanez az analógia figyelhető meg, ha a vezetékek párhuzamosan vannak csatlakoztatva. A feszültség mindegyiken azonos és egyenlő azzal, amelyik mindegyiken egyszerre van. A teljes feszültség képlete:
U gen=U 1=U 2
Az elektromos ellenállás képletei
Már nem tudod megjegyezni őket, de ismered az Ohm-törvény képletét, és abból származtathatod a kívántat. Ebből a törvényből az következika feszültség egyenlő az áramerősség és az ellenállás szorzatával. Azaz U=IR, ahol R az ellenállás.
Akkor a képlet, amellyel dolgoznia kell, a vezetékek csatlakoztatásának módjától függ:
- sorosan, tehát egyenlőségre van szükség a feszültséghez - IgenRösszesen=I1R1 + I2R2;
- párhuzamosan az áramerősség képletét kell használni - Uösszesen / Rösszesen=U 1/ R1 + U2 / R2 .
Egyszerű átalakítások követik, amelyek azon a tényen alapulnak, hogy az első egyenlőségben az összes áram értéke azonos, a másodikban pedig a feszültségek egyenlőek. Így lerövidíthetők. Vagyis a következő kifejezéseket kapjuk:
- R gen=R 1 + R 2 (a vezetékek soros csatlakoztatásához)
- 1 / R gen=1 / R 1 + 1 / R 2(ha párhuzamosan van csatlakoztatva).
Amikor a hálózathoz csatlakoztatott ellenállások száma növekszik, a kifejezésekben szereplő kifejezések száma megváltozik.
Érdemes megjegyezni, hogy a vezetékek párhuzamos és soros kötése eltérő hatással van a teljes ellenállásra. Az első csökkenti az áramköri szakasz ellenállását. Sőt, kiderül, hogy kisebb, mint a legkisebb használt ellenállás. Sorba kapcsolva minden logikus: az értékek összeadódnak, így mindig a teljes szám lesz a legnagyobb.
Aktuális munka
Az előző három mennyiség alkotja a párhuzamos kapcsolódás és a vezetékek soros elrendezésének törvényeit egy áramkörben. Ezért feltétlenül ismerni kell őket. A munkáról és a hatalomról csak emlékeznie kell az alapképletre. A következőképpen van írva: A \u003d IUt, ahol A az áram munkája, t a vezetőn való áthaladásának ideje.
A soros csatlakozással végzett teljes munka meghatározásához ki kell cserélni a feszültséget az eredeti kifejezésben. A következő egyenlőséget kapja: A \u003d I(U 1 + U 2)t, megnyitva a zárójeleket, amelyekből kiderül, hogy a a teljes szakaszon végzett munka megegyezik az egyes aktuális fogyasztók mennyiségével.
Az érvelés hasonlóan halad, ha párhuzamos csatlakozási sémát veszünk figyelembe. Csak az áramerősséget kell cserélni. De az eredmény ugyanaz lesz: A=A 1 + A 2.
Jelenlegi teljesítmény
Egy áramköri szakasz teljesítményképletének ("P" jelölése) származtatása során ismét egy képletet kell használnia: P \u003d UI. Ilyen okoskodás után kiderül, hogy a párhuzamos és soros kapcsolatok egy ilyen teljesítményképlettel írható le: P \u003d P1 + P 2.
Azaz, függetlenül attól, hogy a sémákat hogyan állítják össze, a teljes teljesítmény a munkában résztvevők összege lesz. Ez magyarázza azt a tényt, hogy lehetetlen egyszerre sok nagy teljesítményű eszközt bevonni a lakáshálózatba. Egyszerűen nem bírja a terhelést.
Hogyan befolyásolja a vezetékek csatlakoztatása az újévi füzér javítását?
Rögtön az egyik izzó kiégése után kiderül, hogyan csatlakoztatták őket. Nál nélsoros kapcsolat esetén egyik sem fog világítani. Ez annak a ténynek köszönhető, hogy a használhatatlanná vált lámpa megszakítja az áramkört. Ezért mindent ellenőriznie kell, hogy megállapítsa, melyik égett ki, cserélje ki - és a füzér elkezd működni.
Ha párhuzamos kapcsolatot használ, akkor nem áll le, ha valamelyik izzó meghibásodik. Végül is a lánc nem lesz teljesen eltörve, hanem csak egy párhuzamos rész. Egy ilyen füzér megjavításához nem kell az áramkör összes elemét ellenőriznie, csak azokat, amelyek nem világítanak.
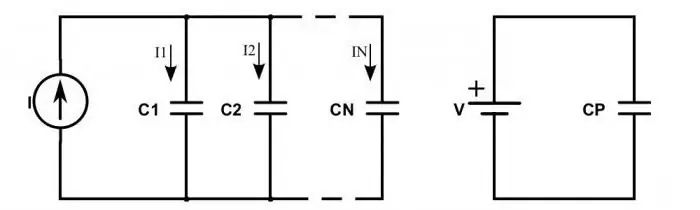
Mi történik az áramkörrel, ha az ellenállások helyett kondenzátorokat tartalmaznak?
Amikor sorba vannak kötve, a következő helyzet figyelhető meg: az áramforrás pluszjaiból származó töltések csak a szélső kondenzátorok külső lemezeire jönnek. A közöttük lévők egyszerűen továbbítják a töltést a láncon. Ez magyarázza azt a tényt, hogy ugyanazok a töltések jelennek meg az összes lemezen, de eltérő előjelekkel. Ezért minden sorba kapcsolt kondenzátor elektromos töltése a következőképpen írható fel:
q gen =q 1=q 2.
Az egyes kondenzátorok feszültségének meghatározásához ismernie kell a következő képletet: U=q / C. Ebben a C a kondenzátor kapacitása.
A teljes feszültség ugyanazt a törvényt követi, mint az ellenállásoké. Ezért a kapacitásképletben a feszültséget az összeggel helyettesítve azt kapjuk, hogy az eszközök teljes kapacitását a következő képlettel kell kiszámítani:
C=q / (U 1 + U2).
Egyszerűsítheti ezt a képletet, ha átfordítja a törteket, és a feszültség/töltés arányát kapacitásra cseréli. A következő egyenlőség adódik: 1 / С=1 / С 1 + 1 / С 2.
A helyzet némileg másképp néz ki, ha a kondenzátorok párhuzamosan vannak csatlakoztatva. Ezután a teljes töltést az összes eszköz lemezén felhalmozódó összes töltés összege határozza meg. És a feszültség értékét továbbra is az általános törvények szerint határozzák meg. Ezért a párhuzamosan kapcsolt kondenzátorok teljes kapacitásának képlete:
С=(q 1 + q 2) / U.
Azaz ez az érték a kapcsolathoz használt egyes eszközök összegének számít:
S=S 1 + S 2.
Hogyan határozható meg a vezetékek tetszőleges csatlakoztatásának teljes ellenállása?
Azaz olyan, amelyben egymást követő szakaszok helyettesítik a párhuzamosakat, és fordítva. Számukra továbbra is az összes leírt törvény érvényes. Csak Önnek kell ezeket szakaszosan alkalmaznia.
Először is állítólag mentálisan kiterjeszti a rendszert. Ha nehéz elképzelni, akkor le kell rajzolnia, mi történik. A magyarázat világosabb lesz, ha egy konkrét példán keresztül megvizsgáljuk (lásd az ábrát).
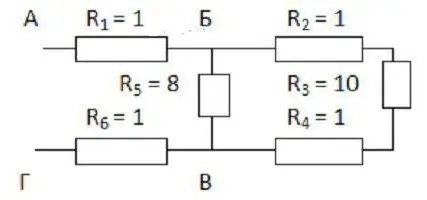
A rajzolást célszerű a B és C pontból kezdeni. Ezeket egymástól és a lap széleitől bizonyos távolságra kell elhelyezni. A bal oldalon egy vezeték megközelíti a B pontot, kettő pedig már jobbra van irányítva. A B pontnak viszont két ága van a bal oldalon, és egy vezeték utána.
Most ki kell töltenie a köztük lévő helyetpontok. A felső vezeték mentén három 2-es, 3-as és 4-es együtthatójú ellenállást kell elhelyezni, alulról pedig az 5-ös indexűt kell elhelyezni. Az első három sorba van kötve. Az ötödik ellenállással párhuzamosak.
A fennmaradó két ellenállás (az első és a hatodik) sorba van kötve a BV vizsgált szakaszával. Ezért a rajz egyszerűen kiegészíthető két téglalappal a kiválasztott pontok két oldalán. Marad az ellenállás kiszámítására szolgáló képletek alkalmazása:
- először a soros csatlakozáshoz megadott;
- akkor párhuzamosan;
- és újra egymás után.
Ily módon bármilyen, még nagyon összetett sémát is telepíthet.
A vezetékek soros csatlakoztatásának problémája
Állapot. Két lámpa és egy ellenállás van egymás mögött egy áramkörben csatlakoztatva. A teljes feszültség 110 V, az áramerősség pedig 12 A. Mekkora az ellenállás értéke, ha minden lámpa névleges 40 V?
Döntés. Mivel soros kapcsolatról van szó, a törvényeinek képletei ismertek. Csak helyesen kell alkalmazni őket. Kezdje azzal, hogy megtudja az ellenálláson lévő feszültség értékét. Ehhez ki kell vonni egy lámpa feszültségének kétszeresét a teljes értékből. Kiderült, hogy 30 V.
Most, hogy két mennyiség ismert, az U és az I (a második a feltételben van megadva, mivel a teljes áram egyenlő az egyes soros fogyasztók áramával), kiszámíthatjuk az ellenállás ellenállását a segítségével Ohm törvénye. Kiderült, hogy 2,5 ohm.
Válasz. Az ellenállás ellenállása 2,5 ohm.
Feladatpárhuzamos és soros kondenzátorok csatlakoztatásához
Állapot. Három kondenzátor van, amelyek kapacitása 20, 25 és 30 mikrofarad. Határozza meg a teljes kapacitásukat sorosan és párhuzamosan csatlakoztatva.
Döntés. Párhuzamos kapcsolattal egyszerűbb kezdeni. Ebben a helyzetben mindhárom értéket csak össze kell adni. Így a teljes kapacitás 75uF.
A számítások valamivel bonyolultabbak lesznek, ha ezeket a kondenzátorokat sorba kötik. Végül is először meg kell találni az egység arányát ezekhez a kapacitásokhoz, majd össze kell adni őket. Kiderült, hogy az egység osztva a teljes kapacitással 37/300. Ekkor a kívánt érték körülbelül 8 mikrofarad.
Válasz. A teljes kapacitás soros csatlakozásnál 8 uF, párhuzamosan - 75 uF.






