A piramis prizmával együtt tökéletes poliéder a háromdimenziós térben, geometriai jellemzőit a középiskolában tanulják. Ebben a cikkben megvizsgáljuk, hogy melyek a piramisok, milyen elemekből állnak, és röviden jellemezzük a helyes piramisokat.
Geometrikus alakpiramis
A geometria szempontjából a piramis egy térbeli alakzat, amely egy sokszögből és több háromszögből áll. Ennek a figurának a megszerzése meglehetősen egyszerű. Ehhez vegyünk egy n oldalú sokszöget, majd válasszunk egy tetszőleges pontot a térben, amely nem a sokszög síkjában lesz, és a sokszög minden csúcsát kötjük ehhez a ponthoz. Nyilvánvaló, hogy az így kialakított alaknak n darab háromszöge lesz, amelyek egy csúcsban kapcsolódnak egymáshoz.
A leírt ábra geometriai alakjának megjelenítéséhez készítsünk egy képet.

Ez egy négyszögletű piramist mutat, amelynek az alapjanégyszög, és az oldalfelületet négy háromszög alkotja, amelyeknek közös csúcsuk van.
Piramiselemek
Mint minden poliéder, a piramist is háromféle elem alkotja:
- élek;
- csúcsok;
- bordák.
Az arcok olyan síkok részei, amelyek elválasztják az alakzat belső térfogatát a környező tértől. Ha a piramis alapja n-szöget tartalmaz, akkor lapjainak száma mindig n+1. Ezek közül n oldal háromszög alakú, és az egyik oldal az említett n-szögű alap.
A csúcsok olyan pontok, ahol egy alak három vagy több lapja metszi egymást. Az alapterület n csúcsot tartalmaz, amelyek mindegyikét két háromszöglap és egy alap alkotja. Azt a pontot, ahol n háromszög oldal találkozik, a piramis csúcsának nevezzük. Így a vizsgált ábra n+1 csúcsból áll.
Az élek egyenes vonalak, amelyek akkor jelennek meg, amikor két lap metszi egymást. Minden élt két csúcs határol a végein. Minden n-szögű alappal rendelkező piramis 2n élt tartalmaz. Ennek a számnak a felét, azaz n-t kizárólag az oldalsó háromszögek metszéspontja alkotja.
Lehetséges figuratípusok
A vizsgált ábra nevét egyedileg határozza meg az alján lévő sokszög típusa. Például, ha három sarka és három oldala van, akkor a piramis háromszög alakú lesz, ha négy - négyszögletes, és így tovább.
A sokszög lehet domború és konkáv, valamint szabályos és általános típusú. Mindez meghatározza a piramis megjelenését is.
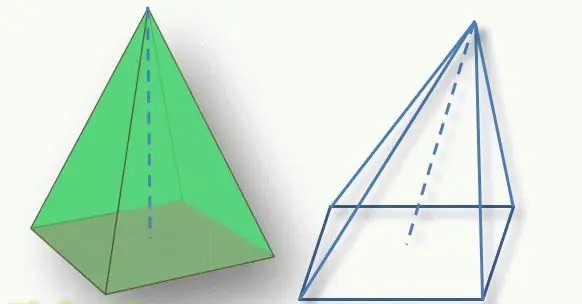
A figura típusának meghatározásánál fontos szempont a piramis csúcsának az alapjához viszonyított helyzete. A felülről a sokszög alapjára húzott merőleges szakaszt az ábra magasságának nevezzük. Ha ez a szakasz az alapot a geometriai középpontjában metszi (háromszögnél ez a mediánok metszéspontja, négyszögnél az átlók metszéspontja), akkor az ábrát egyenesnek nevezzük. Egyébként ferde piramisról beszélnek.
Ha az alap n-szöge szabályos (egyenlő oldalú háromszög, négyzet stb.), és az ábra egyenes, akkor szabályos gúlának nevezzük.
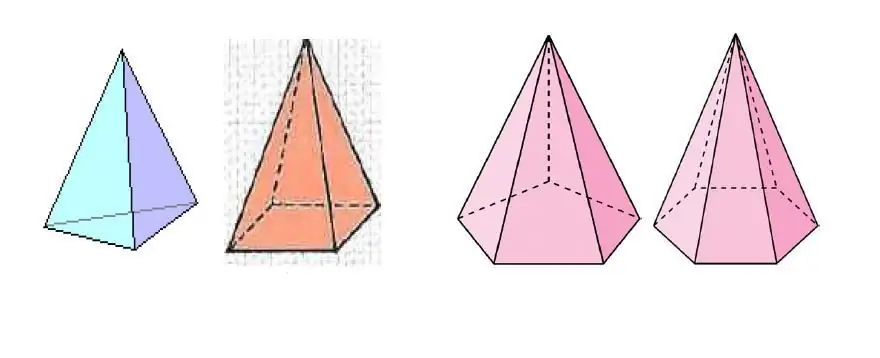
A fenti képen több piramis látható, amelyek a sokszög oldalainak számában különböznek az alapnál.
Szabályos piramisok tulajdonságai
Ezek a piramisok nagyfokú szimmetriával különböznek az osztály többi alakjától. Ebben a tekintetben kényelmes különféle geometriai számításokat végezni velük, például térfogatra vagy felületre vonatkozóan.
Egy szabályos piramis tövében egy n-szög található, amelynek területét az oldala hosszának ismeretében egyedileg határozzuk meg. Az ábra oldalfelületét n darab egyforma háromszög alkotja, amelyek egyenlő oldalúak. Az oldalfelületen elhelyezkedő szabályos gúla élei egyenlőek egymással. Ennek az élnek a hosszának értékét gyakran használják egy alakzat apotémjének kiszámításakor és a felület meghatározásakor.
Egy szabályos gúla magassága az ábra második fontos jellemzője (az első az él hosszaindokok). A magasság a hangerő kiszámításakor használatos.
Bármely, az alappal párhuzamos sík, amely metszi a gúla oldallapjait, sokszögű metszet kialakításához vezet. Az alapsokszöghez képest homotetikus. A leírt szeletművelet új figurák egész osztályának - csonka szabályos piramisok - kialakulásához vezet.
A leghíresebb piramisok

Természetesen ezek az egyiptomi fáraók szabályos négyszögletű piramisai. A Giza nevű helyen több mint 100 ilyen kőemlék található, amelyek kialakításának tökéletessége és geometriai paramétereinek pontossága a mai napig ámulatba ejti a tudósokat. A legnagyobb közülük a Kheopsz piramis, amely körülbelül 146 méter magas és körülbelül 230 méter hosszú.
Mit szolgáltak pontosan ezek a piramisok, valamint azt, hogy milyen mechanizmusokkal és mikor épültek, a mai napig senki sem tudja.






