Mint Ön is tudja, bármely fizikai mennyiség két típus egyikéhez tartozik: skalár vagy vektor. Ebben a cikkben olyan kinematikai jellemzőket fogunk figyelembe venni, mint a sebesség és a gyorsulás, és azt is megmutatjuk, hová irányulnak a gyorsulás- és sebességvektorok.
Mi a sebesség és a gyorsulás?
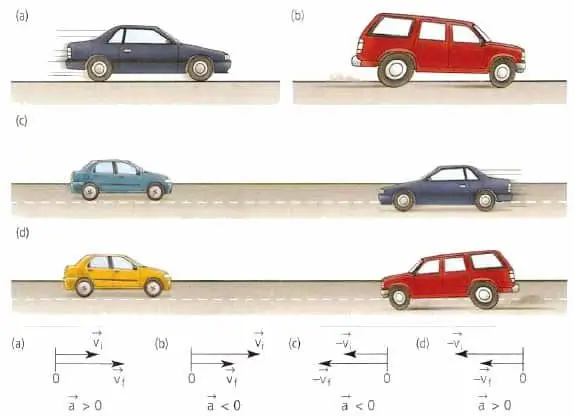
Mindkét, ebben a bekezdésben említett mennyiség fontos jellemzője bármilyen mozgásnak, akár egyenes vonalban, akár íves pályán mozgatja a testet.
A sebesség az a sebesség, amellyel a koordináták idővel változnak. Matematikailag ez az érték egyenlő a megtett távolság időbeli deriváltjával, azaz:
v¯=dl¯/dt.
Itt az l¯ vektort az útvonal kezdőpontjától a végpontig irányítjuk.
A gyorsulás viszont az a sebesség, amellyel maga a sebesség változik az időben. Képlet formájában a következőképpen írható fel:
a¯=dv¯/dt.
Nyilvánvalóan a második származékát vével¯ elmozdulásvektor időben, akkor a gyorsulás értékét is megkapjuk.
Mivel a sebességet méter per másodpercben mérik, a gyorsulást az írott kifejezés szerint méter per másodperc négyzetben mérik.

Hol vannak a gyorsulás- és sebességvektorok?
A fizikában a test bármely mechanikai mozgását általában egy bizonyos pálya jellemzi. Ez utóbbi egy képzeletbeli görbe, amely mentén a test mozog a térben. Például egy egyenes vagy egy kör kiváló példa a gyakori mozgási pályákra.
A test sebességvektora mindig a mozgás irányába irányul, függetlenül attól, hogy a test lassul vagy gyorsul, egyenes vonalban vagy ívben mozog. Geometriai értelemben a sebességvektor tangenciálisan irányul annak a pályának a pontjára, amelyben a test jelenleg található.
Egy anyag vagy testpont gyorsulási vektorának semmi köze a sebességhez. Ez a vektor a sebességváltozás irányába irányul. Például egyenes vonalú mozgás esetén az a¯ érték vagy egybeeshet v¯-vel, vagy ellentétes lehet v¯-vel.
A testre ható erő és a gyorsulás
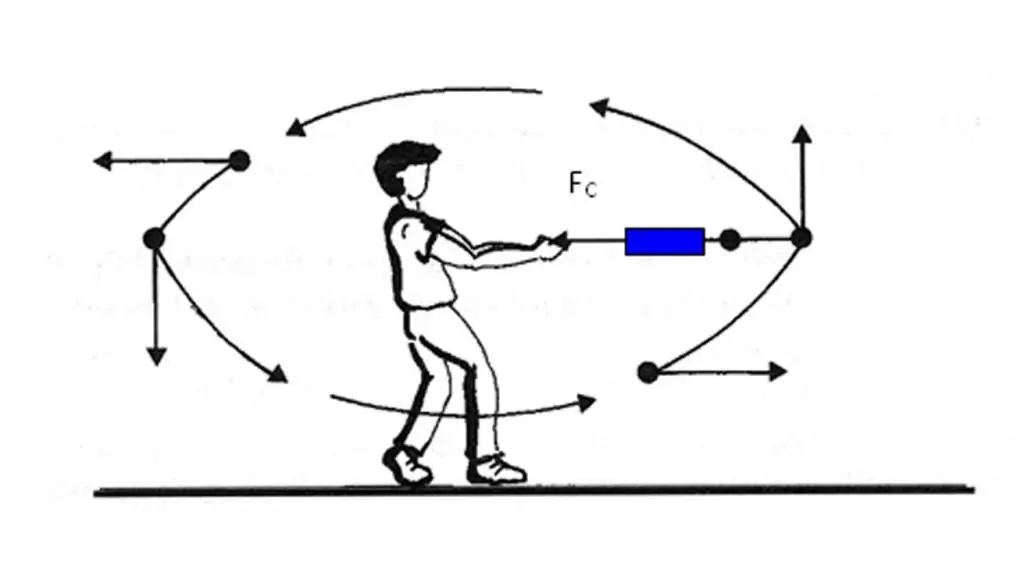
Megtaláltuk, hogy a test gyorsulási vektora a sebességvektor változása felé irányul. Azt azonban nem mindig könnyű meghatározni, hogy a pálya adott pontján hogyan változik a sebesség. Ezenkívül a sebesség változásának meghatározásához szükséges a művelet végrehajtásavektor különbségek. Hogy elkerüljük ezeket a nehézségeket az a¯ vektor irányának meghatározásában, van egy másik módja annak, hogy gyorsan kiderítsük.
Alább található Newton híres és minden diák számára jól ismert törvénye:
F¯=ma¯.
A képlet azt mutatja, hogy a testekben a gyorsulás oka a rájuk ható erő. Mivel az m tömeg skalár, az F¯ erővektor és az a¯ gyorsulásvektor azonos irányú. Ezt a tényt emlékezni kell és alkalmazni kell a gyakorlatban, amikor szükség van az a¯ mennyiség irányának meghatározására.
Ha több különböző erő hat a testre, akkor a gyorsulási vektor iránya megegyezik az összes erő eredő vektorával.
Körmozgás és gyorsulás
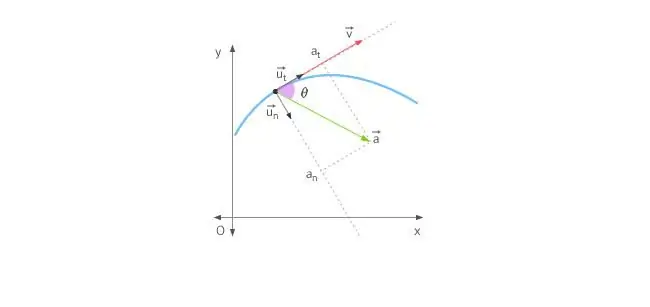
Amikor egy test egyenes vonalban mozog, a gyorsulás előre vagy hátra irányul. Körben történő mozgás esetén a helyzetet bonyolítja, hogy a sebességvektor folyamatosan változtatja irányát. A fentiekre tekintettel a teljes gyorsulást annak két összetevője határozza meg: a tangenciális és normál gyorsulások.
Az érintőleges gyorsulás pontosan ugyanúgy irányul, mint a sebességvektor, vagy ellene. Más szóval, ez a gyorsulási komponens a pálya érintője mentén irányul. A tangenciális gyorsulás maga a sebesség modulusának változását írja le.
A normál gyorsulás a normál mentén irányul a pálya adott pontjára, annak görbületét figyelembe véve. Körkörös mozgás esetén ennek a komponensnek a vektora jelzia középpontba, vagyis a normál gyorsulás a forgási sugár mentén irányul. Ezt az összetevőt gyakran centripetálisnak nevezik.
A teljes gyorsulás ezeknek az összetevőknek az összege, így vektora tetszőlegesen irányítható a körvonalhoz képest.
Ha a test a lineáris sebesség megváltoztatása nélkül forog, akkor csak egy nullától eltérő normálkomponens van, tehát a teljes gyorsulásvektor a kör közepe felé irányul. Vegyük észre, hogy erre a központra is hat olyan erő, amely a testet a pályáján tartja. Például a Nap gravitációs ereje pályájukon tartja Földünket és más bolygókat.






