Ma cikkünk témája egy anyagi pont kinematikája lesz. Miről van szó? Milyen fogalmak jelennek meg benne, és milyen definíciót kell adni ennek a kifejezésnek? Ma megpróbálunk választ adni ezekre és sok más kérdésre.
Definíció és fogalom
Egy anyagi pont kinematikája nem más, mint a fizika "mechanikának" nevezett alszaka. Ő viszont bizonyos testek mozgási mintáit tanulmányozza. Az anyagi pont kinematikája is foglalkozik ezzel a problémával, de nem általánosan. Valójában ez az alfejezet olyan módszereket tanulmányoz, amelyek lehetővé teszik a testek mozgásának leírását. Ebben az esetben csak az úgynevezett idealizált testek alkalmasak kutatásra. Ezek közé tartozik: egy anyagi pont, egy abszolút merev test és egy ideális gáz. Tekintsük részletesebben a fogalmakat. Az iskolapadból mindannyian tudjuk, hogy anyagi pontot szokás olyan testnek nevezni, amelynek méretei adott helyzetben elhanyagolhatók. Egyébként egy anyagi pont transzlációs mozgásának kinematikája először kezdődikhetedik osztályos fizika tankönyvekben jelennek meg. Ez a legegyszerűbb ág, így a legkényelmesebb a tudománnyal való ismerkedést a segítségével kezdeni. Külön kérdés, hogy mik az anyagi pont kinematikájának elemei. Elég sok van belőlük, és feltételesen több, különböző bonyolultságú szintre oszthatók a megértéshez. Ha például a sugárvektorról beszélünk, akkor annak meghatározásában elvileg nincs semmi túl bonyolult. Abban azonban egyetértesz, hogy egy diáknak sokkal könnyebb lesz megértenie, mint egy középiskolásnak vagy középiskolásnak. És hogy őszinte legyek, nem kell elmagyarázni ennek a kifejezésnek a jellemzőit a középiskolásoknak.
A kinematika létrejöttének rövid története
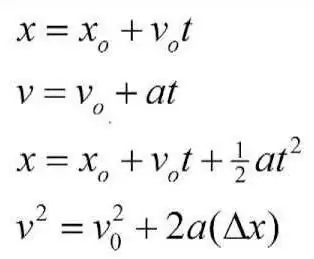
Sok-sok évvel ezelőtt a nagy tudós, Arisztotelész szabadidejének oroszlánrészét a fizika mint külön tudomány tanulmányozásának és leírásának szentelte. A kinematikával is foglalkozott, igyekezett bemutatni annak főbb téziseit és fogalmait, így vagy úgy, ahogyan a gyakorlati, sőt a mindennapi problémák megoldására is használják. Arisztotelész adta a kezdeti elképzeléseket arról, hogy mik az anyagi pont kinematikájának elemei. Művei és művei nagyon értékesek az egész emberiség számára. Mindazonáltal következtetéseiben jelentős számú hibát vétett, aminek oka bizonyos tévhitek és téves számítások voltak. Egy időben egy másik tudós, Galileo Galilei érdeklődött Arisztotelész munkái iránt. Arisztotelész egyik alapvető tézise az volt, hogy a test mozgásacsak akkor következik be, ha valamilyen erő hat rá, amelyet az intenzitás és az irány határoz meg. Galilei bebizonyította, hogy ez hiba volt. Az erő befolyásolja a mozgási sebesség paramétert, de nem többet. Az olasz megmutatta, hogy az erő az oka a gyorsulásnak, és csak kölcsönösen keletkezhet vele. Galileo Galilei emellett jelentős figyelmet fordított a szabadesés folyamatának tanulmányozására, levezetve a megfelelő mintákat. Valószínűleg mindenki emlékszik híres kísérleteire, amelyeket a pisai ferde toronyban végzett. A fizikus Ampère a kinematikai megoldások alapjait is felhasználta munkáiban.
Kiinduló koncepciók
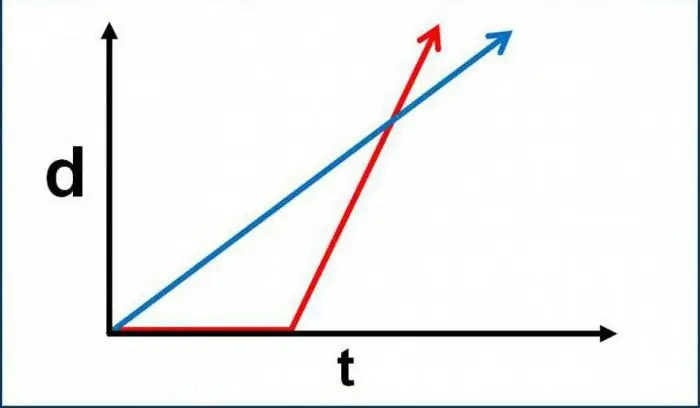
Amint korábban említettük, a kinematika az idealizált objektumok mozgásának leírásának módjait tanulmányozza. Ebben az esetben a matematikai elemzés alapjai, a hétköznapi algebra és a geometria a gyakorlatban is alkalmazhatók. De milyen fogalmak (pontosabban fogalmak, és nem parametrikus mennyiségek meghatározásai) állnak a fizika ezen alfejezetében? Először is mindenkinek világosan meg kell értenie, hogy egy anyagi pont transzlációs mozgásának kinematikája a mozgást az erőmutatók figyelembevétele nélkül veszi figyelembe. Vagyis a megfelelő problémák megoldásához nincs szükségünk az erővel kapcsolatos képletekre. A kinematika nem veszi figyelembe, függetlenül attól, hogy hányan vannak - egy, kettő, három, legalább több százezer. Ennek ellenére a gyorsulás megléte továbbra is biztosított. Számos feladatban egy anyagi pont mozgásának kinematikája előírja a gyorsulás nagyságának meghatározását. Ennek a jelenségnek az okai azonban (azaz az erők illtermészetüket) nem veszik figyelembe, hanem kihagyják.
Osztályozás
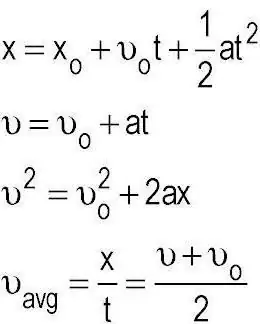
Rájöttünk, hogy a kinematika olyan módszereket kutat és alkalmaz, amelyekkel leírható a testek mozgása, tekintet nélkül a rájuk ható erőkre. Egyébként a mechanika egy másik alszekciója, amit dinamikának neveznek, ilyen feladattal foglalkozik. Már ott is alkalmazzák a Newton-törvényeket, amelyek lehetővé teszik a gyakorlatban, hogy kis mennyiségű ismert kiindulási adattal elég sok paramétert határozzunk meg. Az anyagi pont kinematikájának alapfogalmai a tér és az idő. És a tudomány általános és ezen a területen történő fejlődésével kapcsolatban felmerült a kérdés, hogy helyénvaló-e egy ilyen kombináció alkalmazása.
A kezdetektől fogva klasszikus kinematika volt. Elmondhatjuk, hogy nemcsak az időbeli és térbeli rések jelenléte jellemzi, hanem az egyik vagy másik vonatkoztatási rendszer megválasztásától való függetlenség is. Erről egyébként egy kicsit később lesz szó. Most pedig magyarázzuk el, miről is beszélünk. Ebben az esetben egy szakaszt térbeli intervallumnak, egy időintervallumot pedig időintervallumnak tekintünk. Úgy tűnik, minden világos. Tehát ezeket a hiányosságokat a klasszikus kinematikában abszolútnak, invariánsnak tekintjük, más szóval, függetlennek az egyik vonatkoztatási rendszerről a másikra való átmenettől. Legyen szó üzleti relativisztikus kinematikáról. Ebben változhatnak a referenciarendszerek közötti átmenet rései. Még helyesebb lenne azt mondani, hogy nem, de valószínűleg muszáj. Emiatt a kettő egyidejűségea véletlenszerű események is viszonylagossá válnak, és különös figyelmet szentelnek. Ezért van az, hogy a relativisztikus kinematikában két fogalom - a tér és az idő - egyesül egybe.
Az anyagi pont kinematikája: sebesség, gyorsulás és egyéb mennyiségek
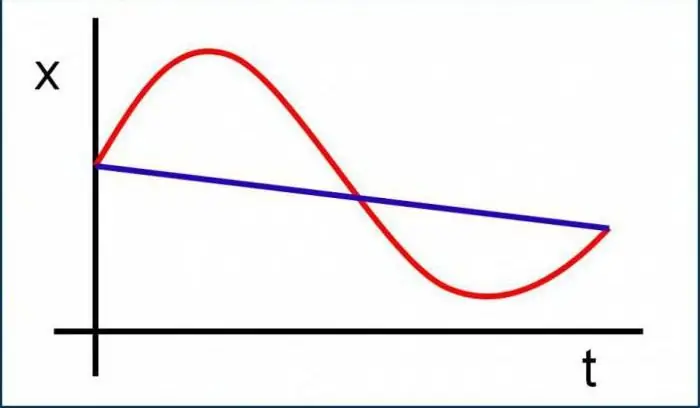
Ahhoz, hogy legalább egy kicsit megértsük a fizika ezen alfejezetét, el kell tájékozódnia a legfontosabb fogalmak között, ismernie kell a definíciókat, és el kell képzelnie, hogy általánosságban mi ez vagy az a mennyiség. Ebben nincs semmi nehéz, sőt, minden nagyon könnyű és egyszerű. Kezdésként talán a kinematikai feladatokban használt alapfogalmakat vegyük figyelembe.
Mozgás
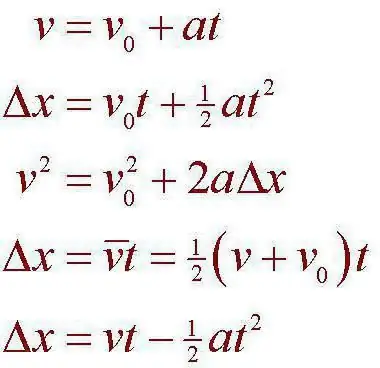
A mechanikus mozgást azt a folyamatot fogjuk figyelembe venni, amelynek során egyik vagy másik idealizált objektum megváltoztatja helyzetét a térben. Ebben az esetben azt mondhatjuk, hogy a változás más testekhez képest történik. Figyelembe kell venni azt is, hogy egy bizonyos időintervallum megállapítása két esemény között egyidejűleg történik. Lehetőség lesz például egy bizonyos intervallum elkülönítésére, amely a test egyik pozícióból a másikba érkezése között eltelt idő alatt alakul ki. Azt is megjegyezzük, hogy a testek ebben az esetben kölcsönhatásba léphetnek egymással, a mechanika általános törvényei szerint. Pontosan ezzel operál leggyakrabban egy anyagi pont kinematikája. A referenciarendszer a következő fogalom, amely elválaszthatatlanul kapcsolódik hozzá.
Koordináták
Szokásos adatoknak nevezhetők, amelyek lehetővé teszik a test helyzetének egy vagy másik időpontban történő meghatározását. A koordináták elválaszthatatlanul kapcsolódnak a referenciarendszer fogalmához, valamint a koordináta-rácshoz. Leggyakrabban betűk és számok kombinációi.
Sugárvektor
A névből már egyértelműnek kell lennie, hogy mi az. Ennek ellenére beszéljünk erről részletesebben. Ha egy pont egy adott pályán mozog, és pontosan ismerjük egy adott vonatkoztatási rendszer kezdetét, akkor bármikor rajzolhatunk egy sugárvektort. Összekapcsolja a pont kezdeti pozícióját a pillanatnyi vagy a végső pozícióval.
Trajektória
Fontos vonalnak fogjuk nevezni, amely egy adott vonatkoztatási rendszerben egy anyagi pont mozgásának eredményeként fektet le.
Sebesség (lineáris és szögletes is)
Ez egy olyan érték, amely meg tudja mondani, hogy a test milyen gyorsan halad át egy adott távolságintervallumon.
Gyorsulás (szög- és lineáris egyaránt)
Megmutatja, hogy milyen törvény alapján és milyen intenzíven változik a test sebességparamétere.
Talán itt vannak - egy anyagi pont kinematikájának fő elemei. Meg kell jegyezni, hogy a sebesség és a gyorsulás is vektormennyiség. Ez pedig azt jelenti, hogy nemcsak jelzésértékűek, hanem irányuk is van. Mellesleg egy irányba és ellentétes irányba is irányíthatók. Az első esetben a test felgyorsul, a másodikban lelassul.
Egyszerű feladatok
Az anyagi pont kinematikája (a sebesség, a gyorsulás és a távolság gyakorlatilag alapvető fogalmak) nemcsak rengeteg feladatot foglal magában, hanem azok sokféle kategóriáját is. Próbáljunk meg megoldani egy meglehetősen egyszerű feladatot a test által megtett távolság meghatározásával.
Tegyük fel, hogy a rendelkezésünkre álló feltételek a következők. A vezető autója a rajtvonalnál áll. A kezelő a zászlóval megadja az engedélyt, és az autó hirtelen felszáll. Határozza meg, fel tud-e dönteni új rekordot a versenyzők versenyében, ha a következő éllovas 7,8 másodperc alatt teljesíti a száz méteres távot. Vegyük az autó gyorsulását 3 méter osztva egy másodperc négyzetével.
Szóval, hogyan lehet megoldani ezt a problémát? Ez elég érdekes, hiszen bizonyos paramétereket nem kell „száraznunk” meghatározni. Felpezsdítik a forgalom és egy bizonyos helyzet, ami diverzifikálja a megoldási, indikátorkeresési folyamatot. De mitől kell vezérelnünk, mielőtt hozzáfogunk a feladathoz?
1. Az anyagi pont kinematikája ebben az esetben biztosítja a gyorsulás használatát.
2. A megoldást a távolságképlet segítségével feltételezzük, mivel annak számértéke megjelenik a feltételekben.
A probléma valójában egészen egyszerűen megoldódott. Ehhez a távolságképletet vesszük: S=VoT + (-) AT ^ 2/2. Mi értelme van? Ki kell derítenünk, mennyi ideig teszi meg a versenyző a kijelölt távot, majd összehasonlítjuk a számot a rekorddal, hogy megtudjuk, megveri-e vagy sem. Ehhez osszuk be az időt, megkapjuk a képletetneki: AT^2 + 2VoT - 2S. Ez nem más, mint egy másodfokú egyenlet. De az autó felszáll, ami azt jelenti, hogy a kezdeti sebesség 0 lesz. Az egyenlet megoldása során a diszkrimináns 2400 lesz. Az idő megtalálásához a gyökérből kell venni. Tegyük a második tizedesjegyig: 48,98 Keressük meg az egyenlet gyökerét: 48,98/6=8,16 másodperc. Kiderült, hogy a sofőr nem fogja tudni megdönteni a meglévő rekordot.






