A Titius-Bode-szabály (néha egyszerűen Bode-törvénynek nevezik) az a hipotézis, hogy egyes pályarendszerekben, köztük a Napban, a testek féltengelyek mentén forognak a bolygósorrendtől függően. A képlet azt sugallja, hogy kifelé nyúlva minden bolygó körülbelül kétszer olyan messze lesz a Naptól, mint az előző.
A hipotézis helyesen jósolta meg a Ceres (az aszteroidaövben) és az Uránusz pályáját, de nem sikerült meghatározni a Neptunusz pályáját, és végül a Naprendszer kialakulásának elmélete váltotta fel. Nevét Johann Daniel Titiusról és Johann Elert Boderól kapta.

Origins
A Bode-törvényt közelítő sorozat első említése David Gregory 1715-ben megjelent Elements of Astronomy című művében található. Ebben ezt írja: „… feltételezve, hogy a Nap és a Föld távolsága tíz egyenlő részre oszlik, ebből a Merkúr távolsága körülbelül négy lesz, a Vénusztól hét, a Marstól tizenöt, a Jupitertől ötvenkettő, és a Szaturnusz kilencvenöttőlHasonló javaslat, valószínűleg Gregory ihlette, megjelenik Christian Wolff 1724-ben megjelent munkájában.
1764-ben Charles Bonnet Contemplation of Nature című könyvében ezt mondta: "Ismerjük a naprendszerünket alkotó tizenhét bolygót [azaz a fő bolygókat és műholdaikat], de nem vagyunk biztosak abban, hogy nincsenek többé." Ehhez Bonnet művének 1766-os fordításában Johann Daniel Titius két saját bekezdést fűzött a 7. oldal aljára és a 8. oldal tetejére. Az új interpolált bekezdés nem található Bonnet eredeti szövegében: az olaszban sem. sem a mű angol fordítását.
Titius felfedezése
Titius közbeiktatott szövegének két része van. Az első a bolygók Naptól való távolságának sorrendjét magyarázza. Tartalmaz néhány szót a Nap és a Jupiter távolságáról is. De ez még nem a szöveg vége.
Érdemes néhány szót ejteni a Titius-Bode szabály képletéről. Ügyeljen a bolygók közötti távolságokra, és derítse ki, hogy szinte mindegyik a testméretüknek megfelelő arányban van elválasztva egymástól. Osszuk el a Nap és a Szaturnusz távolságát 100 résszel; akkor a Merkúrt négy ilyen rész választja el a Naptól; Vénusz - 4 + 3=7 ilyen részre; Föld - 4+6=10; Mars - 4+12=16.
De vegye figyelembe, hogy a Marstól a Jupiterig van eltérés ettől az olyan precíz előrehaladástól. A Marsból 4+24=28 ilyen részből álló tér következik, de eddig egyetlen bolygót sem fedeztek fel ott. De az építész úrnak üresen kell hagynia ezt a helyet? Soha. ÍgyTegyük fel, hogy ez a tér kétségtelenül a Mars még fel nem fedezett holdjaihoz tartozik, és tegyük hozzá, hogy a Jupiter körül talán még van néhány kisebb hold, amelyeket még egyetlen távcső sem látott.

A Bode felemelkedése
1772-ben Johann Elert Bode huszonöt évesen elkészítette Anleitung zur Kenntniss des gestirnten Himmels ("Útmutató a csillagos ég ismeretéhez") csillagászati összefoglalójának második kiadását, amelyhez hozzáadta a következő lábjegyzetet, amely eredetileg nem volt forráskód, de a későbbi verziókban megjegyezték. Bode emlékirataiban találhatunk utalást Titiusra, amely egyértelműen elismeri tekintélyét.

Véleményfogalom
Ez utóbbi bemutatásánál így hangzik a Titius-Bode szabály: ha a Nap és a Szaturnusz távolságát 100-nak vesszük, akkor a Merkúrt négy ilyen rész választja el a Naptól. Vénusz - 4+3=7. Föld - 4+6=10. Mars - 4+12=16.
Most rés van ebben a rendezett folyamatban. A Mars után egy 4+24=28 számítású tér következik, amelyben még egyetlen bolygót sem láttak. Elhihetjük, hogy az univerzum alapítója üresen hagyta ezt a teret? Természetesen nem. Innen 4+48=52 számítás formájában jutunk el a Jupiter távolságához és végül a Szaturnusz távolságához - 4+96=100.

Ez a két állítás az összes specifikus tipológiára és pályasugárra vonatkozóan az ókorból származikcsillagászat. Ezen elméletek közül sok a tizenhetedik század előtti időre nyúlik vissza.
Befolyásolás
Titius Christian Freiherr von Wolff (1679-1754) német filozófus tanítványa volt. A Bonnet művébe beszúrt szöveg második része von Wolff 1723-as, Vernünftige Gedanken von den Wirkungen der Natur című munkáján alapul.
A huszadik századi irodalom a Titius-Bode-szabály szerzőségét egy német filozófusra bízza. Ha igen, Titius tanulhatna tőle. Egy másik régebbi hivatkozást James Gregory írt 1702-ben Astronomiae Physicae et geometryae Elementa című művében, ahol a 4, 7, 10, 16, 52 és 100 bolygótávolságok sorozata a 2 arány geometriai progressziója lett.
Ez Newton legközelebbi képlete, és Benjamin Martin és Thomas Ceard írásaiban is megtalálható volt Bonnet könyvének németországi megjelenése előtt évekkel.
További munka és gyakorlati vonatkozások
Titius és Bode abban reménykedett, hogy a törvény új bolygók felfedezéséhez vezet, és valóban, az Uránusz és a Ceres felfedezése, amelyek távolsága jól egyezik a törvénnyel, hozzájárult a tudományos világ elfogadásához.
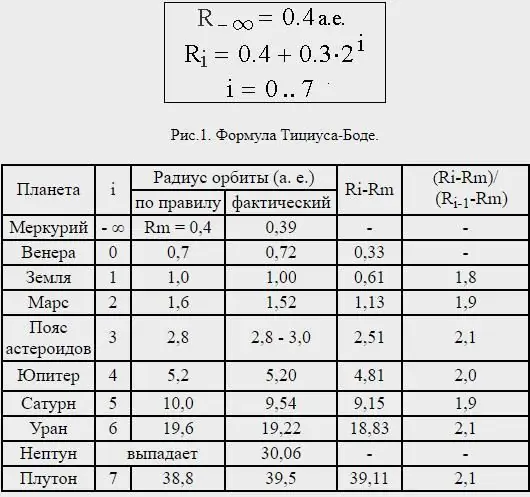
A Neptunusz távolsága azonban nagyon inkonzisztens volt, és valójában a Plútó - ma már nem tekinthető bolygónak - olyan átlagos távolságra van, amely nagyjából megfelel az Uránuszon kívüli következő bolygóra előre jelzett Titius-Bode törvénynek.
Az eredetileg közzétett törvényt az összes ismert bolygó - a Merkúr és a Szaturnusz - megközelítőleg kielégítette, a különbségek közöttnegyedik és ötödik bolygó. Ezt érdekes, de nem nagy jelentőségű alaknak tekintették egészen az Uránusz 1781-es felfedezéséig, ami beleillik a sorozatba.
E felfedezés alapján Bode egy ötödik bolygó felkutatását kérte. A Cerest, az aszteroidaöv legnagyobb objektumát Bode előre jelzett helyén találták meg 1801-ben. Bode törvényét széles körben elfogadták egészen a Neptunusz 1846-os felfedezéséig, és kiderült, hogy nem egyeztethető össze a törvénnyel.
Ugyanakkor az övben felfedezett kisbolygók nagy száma átlépte a Cerest a bolygók listáján. Bode törvényét Charles Sanders Peirce csillagász és logikus tárgy alta 1898-ban a téves érvelés példájaként.

A probléma kialakulása
A Plútó 1930-as felfedezése tovább bonyolította a problémát. Annak ellenére, hogy ez nem felelt meg a Bode-törvény által megjósolt pozíciónak, arról szólt, hogy a törvény a Neptunusznak megjósolta. A Kuiper-öv későbbi felfedezése, és különösen az Eris objektum, amely nagyobb tömegű, mint a Plútó, de nem felel meg Bode törvényének, tovább hiteltelenítette a képletet.
Serda hozzájárulása
Thomas Cerda jezsuita 1760-ban Barcelonában tartotta a híres csillagászati tanfolyamot a Sant Jaume de Cordelle Főiskola (Cordell Nemeseinek Császári és Királyi Szeminárium) Matematikai Tanszékén. Cerdas Tratado-jában a bolygótávolságok jelennek meg, amelyeket Kepler harmadik törvényének alkalmazásával kapunk, 10-3 pontossággal.
Ha 10-nek vesszük a Földtől mért távolságot ésegész számra kerekítve, geometriai progresszió [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2, n=2-től n=8-ig, kifejezhető. És a Kepler-anomália körkörös egyenletes fiktív mozgásával az egyes bolygók arányainak megfelelő Rn értékeket a következőképpen kaphatjuk meg: rn=(Rn - R1) / (Rn-1 - R1), ami 1,82; 1, 84; 1, 86; 1,88 és 1,90, ahol rn=2 - 0,02 (12 - n) egy explicit összefüggés a Kepleri kontinuitás és a Titius-Bode törvény között, amelyet véletlen numerikus egybeesésnek tekintünk. A számítás eredménye közel van a kettőhöz, de a kettős szám 1, 82 kerekítésének tekinthető.

A bolygó átlagos sebessége n=1-ről n=8-ra csökkenti a Naptól való távolságot, és eltér az n=2-nél mért egyenletes csökkenéstől, hogy n=7-ről helyreálljon (pályarezonancia). Ez befolyásolja a Nap és a Jupiter távolságát. Azonban az összes többi objektum közötti távolságot a hírhedt szabály keretein belül, amelynek a cikket szentelték, szintén ez a matematikai dinamika határozza meg.
Elméleti szempont
Nincs szilárd elméleti magyarázat a Titius-Bode szabály alapjául, de lehetséges, hogy a pályarezonancia és a szabadsági fokok hiánya kombinációját figyelembe véve bármely stabil bolygórendszer nagy valószínűséggel megismétli a 2008-ban leírt modellt. ez az elmélet a két tudóstól.
Mivel ez matematikai véletlen egybeesés, és nem „természettörvény”, néha inkább szabálynak nevezik, mint „törvénynek”. Alan Boss asztrofizikus azonban azzal érvel, hogy ez egyszerűenEgybeesés, és az Icarus bolygótudományi folyóirat többé nem fogad el olyan cikkeket, amelyek megpróbálják a „törvény” továbbfejlesztett változatát közölni.
Orbitális rezonancia
A főbb keringő testek orbitális rezonanciája olyan régiókat hoz létre a Nap körül, amelyeknek nincs hosszú távú stabil pályájuk. A bolygókeletkezési szimulációs eredmények alátámasztják azt az elképzelést, hogy egy véletlenszerűen kiválasztott stabil bolygórendszer valószínűleg megfelel a Titius-Bode szabálynak.

Dubrulle és Graner
Dubrulle és Graner megmutatta, hogy a hatványtörvény távolságszabályai a bolygórendszerek összeomló felhőinek modelljeinek következményei lehetnek, amelyeknek két szimmetriája van: a forgási invariancia (a felhő és tartalma tengelyszimmetrikus) és a skála invarianciája (a felhő és tartalma minden léptékben ugyanúgy néz ki).
Ez utóbbi számos olyan jelenség jellemzője, amelyekről úgy gondolják, hogy szerepet játszanak a bolygó kialakulásában, mint például a turbulencia. A Nap és a Naprendszer bolygói közötti távolságát, amelyet Titius és Bode javasolt, nem vizsgálták felül Dubrulle és Graner tanulmányai.






