Annak érdekében, hogy a valóságban nem túl „kényelmes” méretű tárgyakat papíron lehessen ábrázolni, az emberek egy mérleget találtak ki. Valójában ez megmagyarázza, mire való a skála.
Amikor az iskolai tanterv elkezdi feltárni a skála fogalmát
A gyerekek először találkoznak ezzel a szóval, miközben a terület térképeit és terveit tanulmányozzák. A tanár elmagyarázza, miért van szükség a mérlegre, mit mutat, az atlaszok példáján. Elmagyarázzák, hogy bármely földrajzi elem olyan nagy, hogy nehéz és kényelmetlen lenne teljes méretben ábrázolni.
Az emberek kicsinyített formában rajzolták meg a terepet, de ehhez nem használtak pontos arányokat. Most ez okosabban történik - a térképen minden kötőjelnek és vonalnak van egy mérete, amelyet meg lehet szorozni egy bizonyos számmal, és megtudhatja a valódi hosszúságot és szélességet.
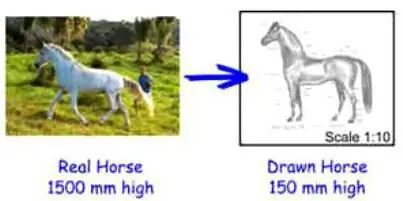
Rekord skála: az olvasás első módja
A skálát kettősponttal elválasztott két szám jelzi. Az első számjegy a méretegységeket jelöli az ábrán, a másodikazt jelzi, hogy az ábrán hány valós egység felel meg az első számnak. Például, ha valamelyik terven 1:1000 méretarány van feltüntetve, és a méretegységek centiméterben vannak feltüntetve, akkor az ábrán egy centiméter a valóságban 1000 cm-nek felel meg. Akkor mire való a mérleg? Segítségével nemcsak kicsinyíthet bizonyos objektumokat a grafikai tervben, hanem pontosan kiszámíthatja azok valós méretét is.
A skála felvételének második módja: mi a kényelmes?
A skála kettősponton keresztüli írásának előző módszerét numerikusnak nevezzük. De van egy elnevezett skála is. Rekordja a következő: 1 cm - 20 km. Kiderül, hogy ilyen módon lehet kompaktan felírni hatalmas léptékeket, amelyeket nem több nullás számok fejeznek ki, ha olyan helyzet állt elő, amikor több száz kilométert kell megadni egy centiméterben. Ugyanakkor rögtön látszik, hogy mennyit, miben és miben. Ez a felvétel intuitívabb és áttekinthetőbb.
Méretezés a rajzban: mi egészíti ki a korábban tanulmányozott koncepciót
A lépték fogalmával nemcsak a földrajzban találkozunk, hanem egy olyan tantárgy tanulmányozása során is, mint a rajz. Ugyanazokat az elveket alkalmazzák a különböző tárgyak ábrázolására. De van egy lényeges különbség: itt a méretarány fogalmát az is kibővíti, hogy kis részleteket nagyobb léptékben is ábrázolhatunk vele. Földrajzban nem erről beszélünk, mert a földrajzban nincsenek olyan kis tárgyak, hogy nagyításra lenne szükség. A kontinensek és hegyek, folyók és tavak mindenesetre nagyobbak, mint egy A4-es papírlap vagy akárA1.
A rajz tanulmányozása során a léptéket használhatja a legkisebb részletek, például csavar vagy fogaskerekek nagyobb méretben történő ábrázolására.
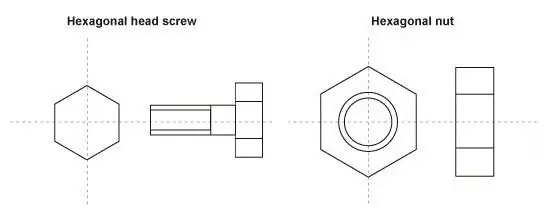
Szóval, ebben az esetben miért van szükség mérlegre? Segítségével kényelmesebben, tisztán és részletesebben ábrázolhat egy kis elemet. Ebben az esetben a jelölésben a fordítottja történik: az első szám nagyobb lesz, mint a második, és a 100:1 jelölés valahogy így hangzik: a kép 100 metrikus egysége a tényleges méret egy egységének felel meg.
Néhány tisztázó példa
Mire való a skála, mit mutat egy kisebb tárgy képe esetén, ami papíron az eredmény? Ismét megvan az alkatrész és a valós tárgy képének méretaránya. Emlékezzünk vissza ugyanarra a 100:1 arányra. Kiderült, hogy az ábrán száz milliméterben csak egy milliméter van a valódi méretben. Ha egy alkatrész 500 milliméter széles a képen, akkor a tényleges szélessége csak 5 milliméter.
Ha felidézzük az első esetet, egy nagy tárgy egy kisebb példányának lapján lévő kép, az 1:100 méretarány azt jelenti, hogy a kép egy millimétere 100 millimétert tartalmaz a valódi méretből. Tehát, ha egy objektum 80 milliméter hosszú egy rajzon vagy térképen, akkor az objektum tényleges hossza 8000 milliméter lesz. Világos példa arra, hogy mire való a méret, és milyen kényelmes találmánya az emberiségnek.
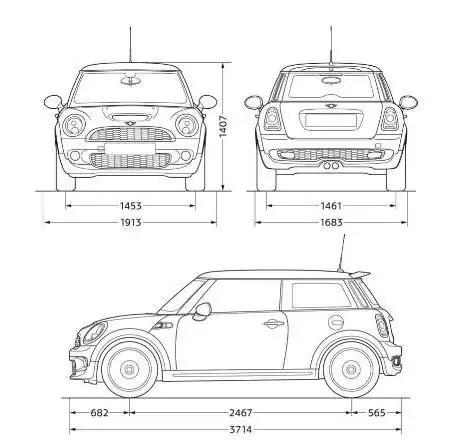
A mérleg használatában az a legfontosabb, hogy azonnalne feledje, hogy az első szám a képre, a második pedig az objektumok tényleges méretére vonatkozik. Annak érdekében, hogy a jövőben ne keveredjenek össze, ezen alapok megszilárdítása érdekében az iskolákban gyakorlati földrajzórákat tartanak, hogy a gyerekek az atlasz segítségével többször elmagyarázzák és kiszámítsák a valós tárgyak méretét. Ugyanez történik a rajzórákon is.
Összegzés
Mire való a skála? A kérdésre adott válasz három pontból áll, amelyeket csak emlékezned kell:
- Először is - a méretarány szükséges a nagyméretű objektumok olyan felületen való megjelenítéséhez, amelyen kényelmes a megtekintés.
- Másodszor - a léptékre a kis tárgyak nagyobb méretben történő ábrázolásához van szükség.
- Harmadik - a léptékre azért van szükség, hogy pontosan meg lehessen határozni egy valódi objektum méretét, függetlenül annak kezdeti méretétől, kicsi vagy nagy.






