Az aggregált halmazállapotú anyagok termodinamikája a fizika egyik fontos ága, amely a rendszerek termodinamikai egyensúlyát és kvázistatikus átmeneteit vizsgálja. A fő modell, amelyen a rendszerek viselkedésére vonatkozó előrejelzések alapulnak, az ideális gázmodell. Használatával a Mengyelejev-Clapeyron egyenletet kaptuk. Vegye figyelembe a cikkben.
Ideális gáz
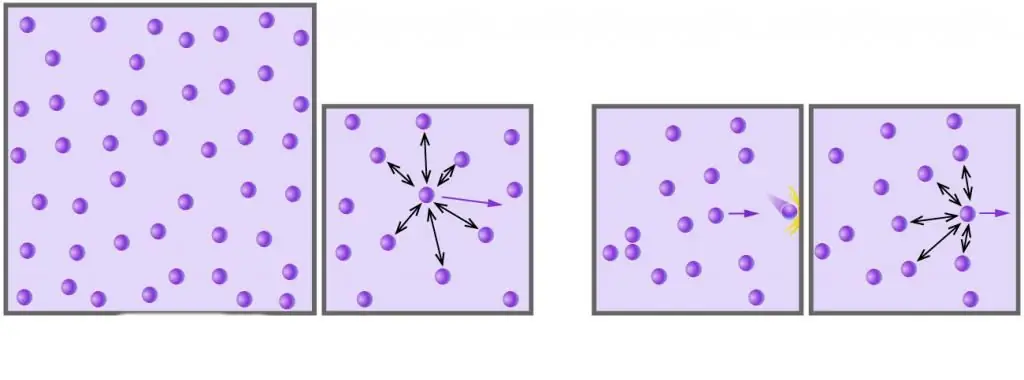
Mint tudod, minden valódi gáz molekulákból vagy atomokból áll, amelyek közötti távolságok túl nagyok az alacsony nyomáson mért méretükhöz képest. Ráadásul magas hőmérsékleten, abszolút skálán a molekulák kinetikus energiája meghaladja a gyenge dipól-dipól kölcsönhatásokhoz kapcsolódó potenciális energiájukat (ha ezeken a kölcsönhatásokon kívül más típusú kémiai kötések is léteznek, pl. ionos ill. hidrogén, akkor jelentős mértékben hozzájárulnak a belső rendszer energia potenciális összetevőjéhez).
MivelSok valódi gáz esetében a normálishoz közeli körülmények között elhanyagolható a belső kölcsönhatásuk és a részecskeméretük. Ez a két fő közelítés alkotja az ideális gázmodellt.
Mengyelejev egyenlete a fizikában

Helyesebb és igazságosabb ezt az egyenletet Clapeyron-Mengyelejev törvénynek nevezni. A helyzet az, hogy először Emile Clapeyron francia mérnök rögzítette 1834-ben. Ezt Boyle-Mariotte, Gay-Lussac és Charles gáztörvényeinek elemzésével tette, amelyeket a 19. század elejére fedeztek fel.
Dmitrij Mengyelejev orosz kémikus érdeme abban rejlik, hogy modern és könnyen használható matematikai formát adott az egyenletnek. Konkrétan Mengyelejev az egyenletbe bevezetett egy állandót minden gázra R=8, 314 J/(molK). Clapeyron maga is számos tapasztalati állandót használt, amelyek megnehezítik a számítási folyamatot.
A Mengyelejev-Clapeyron egyenlet a következőképpen van felírva:
PV=nRT.
Ez az egyenlőség azt jelenti, hogy a P nyomás és a V térfogat szorzata a kifejezés bal oldalán mindig arányos a T abszolút hőmérséklet és a bal oldalon lévő n anyag mennyiségének szorzatával.
A vizsgált kifejezés lehetővé teszi bármely gáztörvény lekérését, ha a négy paraméter közül kettőt javít. Az izofolyamatok esetében olyan zárt rendszereket vizsgálnak, amelyekben nincs anyagcsere a környezettel (n=const). Ezeket a folyamatokat egyetlen rögzített termodinamikai paraméter (T, P vagy V) jellemzi.

Példaprobléma
Most oldjuk meg a Mengyelejev-Clapeyron egyenlet problémáját. Ismeretes, hogy az 500 gramm tömegű oxigén egy 100 literes hengerben van 2 atmoszféra nyomáson. Mennyi a léggömb hőmérséklete, ha a rendszer termodinamikai egyensúlyban van.
Emlékezzünk vissza, hogy a definíció szerint egy anyag mennyiségét a következő képlettel számítjuk ki:
n=m/M.
Ahol m a rendszer összes részecskéjének tömege, M az átlagos moláris tömegük. Ez az egyenlőség lehetővé teszi, hogy a Mengyelejev-egyenletet a következő formában írjuk át:
PV=mRT/M.
Ahonnan megkapjuk a feladat munkaképletét:
T=PVM/(mR).
Az összes mennyiséget át kell váltani SI-mértékegységre, és behelyettesíteni a következő kifejezésbe:
T=21013250, 10, 032/(0, 58, 314)=156 K.
A számított hőmérséklet -117 oC. Bár az oxigén ezen a hőmérsékleten még mindig gáz halmazállapotú (-182,96 oC-on kondenzál), ilyen körülmények között az ideális gázmodell csak a számított érték minőségi becslésére használható.






