A tipikus fényhatások, amelyekkel mindenki gyakran találkozik a mindennapi életben, a tükröződés és a fénytörés. Ebben a cikkben azt az esetet vizsgáljuk meg, amikor mindkét hatás ugyanazon folyamaton belül jelentkezik, a belső teljes reflexió jelenségéről fogunk beszélni.
Fényvisszaverődés
Mielőtt a belső teljes fényvisszaverődés jelenségével foglalkozna, meg kell ismerkednie a közönséges visszaverődés és fénytörés hatásaival. Kezdjük az elsővel. Az egyszerűség kedvéért csak a fényt fogjuk figyelembe venni, bár ezek a jelenségek bármilyen jellegű hullámra jellemzőek.
A reflexió alatt egy egyenes vonalú pálya változását értjük, amely mentén egy fénysugár mozog egy másik egyenes vonalú pályára, amikor útközben akadályba ütközik. Ez a hatás akkor figyelhető meg, ha a lézermutatót a tükörre irányítjuk. Az ég és a fák képeinek megjelenése a vízfelszínre nézve szintén a napfény visszaverődésének eredménye.

A visszaverődésre a következő törvény érvényes: szögeka beesés és a visszaverődés ugyanabban a síkban van a tükröző felületre merőlegesen, és egyenlőek egymással.
Fénytörés
A fénytörés hatása hasonló a visszaverődéshez, csak akkor lép fel, ha a fénysugár útjában álló akadály egy másik átlátszó közeg. Ebben az esetben a kezdeti sugár egy része visszaverődik a felületről, és egy része átmegy a második közegbe. Ezt az utolsó részt megtört nyalábnak nevezzük, és azt a szöget, amelyet a határfelületre merőlegessel bezár, törési szögnek. A megtört sugár ugyanabban a síkban van, mint a visszavert és beeső sugár.
A fénytörés erős példái a ceruza eltörése egy pohár vízben vagy a tó megtévesztő mélysége, amikor az ember lenéz a fenekére.

Matematikailag ezt a jelenséget a Snell-törvény segítségével írják le. A megfelelő képlet így néz ki:
1 sin (θ1)=n2 sin (θ 2).
Itt a beesési és törési szögeket θ1 és θ2-ként jelöljük. Az n1, n2 mennyiségek tükrözik az egyes közegek fénysebességét. Ezeket a közeg törésmutatóinak nevezik. Minél nagyobb n, annál lassabban halad a fény egy adott anyagban. Például a vízben a fény sebessége 25%-kal kisebb, mint a levegőben, ezért a törésmutatója 1,33 (levegőnél 1).
A teljes belső reflexió jelensége
A fénytörés törvénye egyhez vezetérdekes eredmény, amikor a sugár nagy n-es közegből terjed. Vizsgáljuk meg részletesebben, mi történik ebben az esetben a gerendával. Írjuk ki Snell képletét:
1 sin (θ1)=n2 sin (θ 2).
Feltételezzük, hogy n1>n2. Ebben az esetben, hogy az egyenlőség igaz maradjon, θ1 kisebbnek kell lennie, mint θ2. Ez a következtetés mindig érvényes, mivel csak a 0o és 90o közötti szögeket veszik figyelembe, amelyeken belül a szinuszfüggvény folyamatosan növekszik. Így ha sűrűbb optikai közeget hagyunk egy kevésbé sűrűre (n1>n2), a sugár jobban eltér a normáltól.
Most növeljük a θ1 szöget. Ennek eredményeként eljön az a pillanat, amikor θ2 egyenlő lesz 90o-val. Elképesztő jelenség történik: egy sűrűbb közegből kibocsátott nyaláb marad benne, vagyis számára átlátszatlanná válik a határfelület két átlátszó anyag között.
Kritikus szög
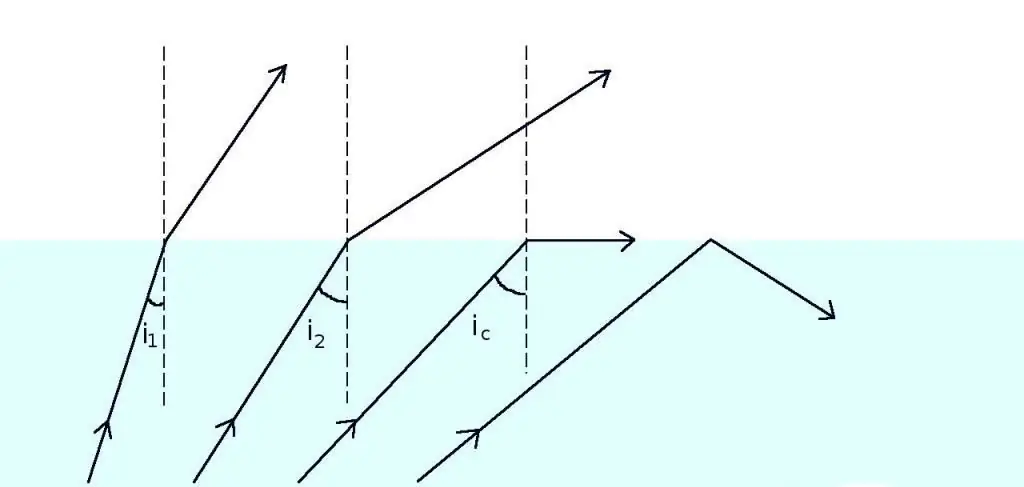
A θ1 szöget, amelyre θ2=90o nevezzük. kritikus a figyelembe vett médiapár számára. Minden olyan sugár, amely a határfelületet a kritikus szögnél nagyobb szögben éri, teljesen visszaverődik az első közegbe. A θc kritikus szögre írhatunk egy kifejezést, amely közvetlenül következik Snell képletéből:
sin (θc)=n2 / n1.
Haa második közeg a levegő, akkor ezt az egyenlőséget a következőre egyszerűsítjük:
sin (θc)=1 / n1.
Például a víz kritikus szöge:
θc=arcsin (1/1, 33)=48, 75o.
Ha a medence aljára merülsz, és felnézel, csak a fejed fölött láthatod az eget és a rajta futó felhőket, a vízfelület többi részén csak a medence falai lesznek láthatóak..
A fenti érvelésből kitűnik, hogy a fénytöréstől eltérően a teljes visszaverődés nem visszafordítható jelenség, csak sűrűbbről kevésbé sűrű közeg felé haladva fordul elő, fordítva viszont nem.
Teljes tükröződés a természetben és a technológiában
Talán a természetben a legáltalánosabb hatás, ami teljes visszaverődés nélkül lehetetlen, a szivárvány. A szivárvány színei a fehér fény esőcseppekben való szétszóródásának eredménye. Amikor azonban a sugarak áthaladnak ezekben a cseppekben, egyszeri vagy kettős belső visszaverődést tapasztalnak. Ezért a szivárvány mindig kettősnek tűnik.
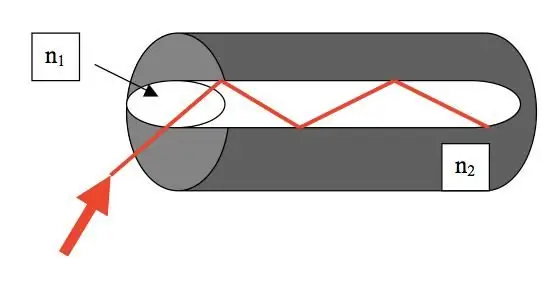
A belső teljes visszaverődés jelenségét az optikai technológiában használják. Az optikai szálaknak köszönhetően az elektromágneses hullámok veszteség nélkül továbbíthatók nagy távolságokra.






