A szakértői értékelés során, például a termékek versenyképességének felmérésekor, mint minden tudományos munkában, statisztikai adatfeldolgozást kell végezni. Ez utóbbi a szakértői vélemények konzisztenciájának meghatározásával kezdődik, melynek számszerű kifejezése a konkordancia együttható.
Miért van szükség szakértői konszenzusos értékelésre?
Ez az értékelés mindenekelőtt azért szükséges, mert a becsült paraméterek tekintetében a szakértői vélemények nagymértékben eltérhetnek. Az értékelés kezdetben a mutatók rangsorolásával és egy bizonyos szignifikancia együttható (súly) hozzárendelésével történik. Az inkonzisztens rangsor azt eredményezi, hogy ezek az együtthatók statisztikailag megbízhatatlanok. A szükséges számú (7-10-nél több) szakértői véleményt a szokásos törvény szerint kell kiosztani.
A konkordancia együttható fogalma
Szóval. A következetesség az összhang. Az együttható egy dimenzió nélküli mennyiség, amely a diszperzió és a maximális diszperzió arányát mutatja általános esetben. Általánosítsuk ezeket a fogalmakat.
A konkordancia együttható egy 0 és 1 közötti szám, amely a szakértői vélemények konzisztenciáját mutatja, amikoregyes ingatlanok rangsorolása. Minél közelebb van ez az érték a 0-hoz, annál kisebb a konzisztencia. Ha ennek az együtthatónak az értéke kisebb, mint 0,3, akkor a szakértői vélemények következetlennek minősülnek. Ha az együttható értéke 0,3 és 0,7 közötti tartományban van, a konzisztenciát átlagosnak tekintjük. A 0,7-nél nagyobb érték nagy konzisztenciának számít.
Használati esetek
Statisztikai kutatások során előfordulhatnak olyan helyzetek, amikor egy objektum nem két, a konkordancia együtthatóval statisztikailag feldolgozott sorozattal jellemezhető, hanem több sorozattal, amelyeket ennek megfelelően azonos szintű szakértők rangsorolnak. professzionalizmus egy bizonyos területen.
Meg kell határozni a szakértők által végzett rangsor következetességét annak a hipotézisnek a helytállóságának igazolására, hogy a szakértők viszonylag pontos méréseket végeznek, ami lehetővé teszi a szakértői csoportokban különböző csoportok kialakítását, amelyeket nagymértékben emberi tényezők határoznak meg, elsősorban a nézetek, fogalmak, különböző tudományos iskolák, a szakmai tevékenység jellege stb. különbségei.
A rangmódszer rövid leírása. Előnyei és hátrányai
A rangsorolásnál a rang módszert használjuk. Lényege abban rejlik, hogy az objektum minden tulajdonságához saját, meghatározott rangot rendelnek. Ezen túlmenően minden szakértői csoportba tartozó szakértő megkapja ezt a rangotönállóan, ami szükségessé teszi ezen adatok feldolgozását a szakértői vélemények következetességének megállapítása érdekében. Ezt a folyamatot a konkordancia együttható kiszámításával hajtjuk végre.
A rangozási módszer fő előnye a könnyű kivitelezés.
A módszer fő hátrányai:
- kevés számú rangsoroló objektum, mivel ha számuk meghaladja a 15-20-at, akkor nehéz objektív rangsorolási pontszámokat adni;
- A módszer alkalmazása alapján nyitva marad az a kérdés, hogy a vizsgált objektumok milyen messze vannak egymástól jelentőségükben.
A módszer alkalmazásakor figyelembe kell venni, hogy a minősítések valamilyen valószínűségi modellen alapulnak, ezért a terjedelemre tekintettel óvatosan kell alkalmazni.
Kendall konkordancia-rangsor-együtthatója
A homogén objektumokat jellemző mennyiségi és minőségi jellemzők közötti kapcsolat meghatározására használják, és ugyanazon elv szerint rangsorolják.
Ezt az együtthatót a következő képlet határozza meg:
t=2S/(n(n-1)), ahol
S - a szekvenciák száma és a második jellemző inverzióinak száma közötti különbségek összege;
n - megfigyelések száma.

Számítási algoritmus:
- Az x értékek növekvő vagy csökkenő sorrendben vannak rangsorolva.
- Az y-értékek abban a sorrendben vannak elrendezve, ahogyan megfelelnek az x-értékeknek.
- Az y minden egymást követő rangjához határozza meg, hogy hány magasabb rangú érték követi azt. Ezeket összeadjuk, és kiszámítjuk az x-ben és y-ban lévő rangsorok megfelelőségének mértékét.
- Hasonlóan az y alacsonyabb értékű rangjainak számát is kiszámítja, amelyek szintén összeadódnak.
- Adja hozzá a magasabb értékű rangok számát és az alacsonyabb értékű rangok számát, így az S értéket kapja.
Ez az együttható két változó közötti kapcsolatot mutatja, és a legtöbb esetben Kendall rangkorrelációs együtthatónak nevezik. Ez a függőség grafikusan ábrázolható.
Együttható meghatározása
Hogyan készül? Ha a rangsorolt jellemzők vagy tényezők száma meghaladja a 2-t, akkor a konkordancia együtthatót használjuk, ami lényegében a rangkorreláció többszörös változata.
Légy óvatos. A konkordancia-együttható számítása a rangok négyzetösszege és a rangok átlagos négyzetösszege 12-vel szorzott eltérésének a szakértői négyzethez viszonyított arányán alapul, szorozva a szám kocka különbségével. az objektumok száma és az objektumok száma.
Számítási algoritmus
Ahhoz, hogy megértsük, honnan származik a 12-es szám a számítási képlet számlálójában, nézzük meg a meghatározási algoritmust.
Minden egyes sorhoz, ahol egy bizonyos szakértő rangja van, a rangok összege kerül kiszámításra, ami egy véletlenszerű érték.
A konkordancia együtthatót általában a varianciabecslés (D) és a varianciabecslés maximális értékének arányaként határozzák meg.(Dmax). Fogalmazzuk meg egymás után ezeknek a mennyiségeknek a definícióit.
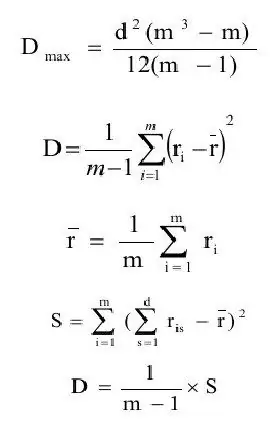
hol rátlag - várható becslés;
m - objektumok száma.
A kapott képleteket D-re behelyettesítve D-remax megkapjuk a konkordancia együttható végső képletét:
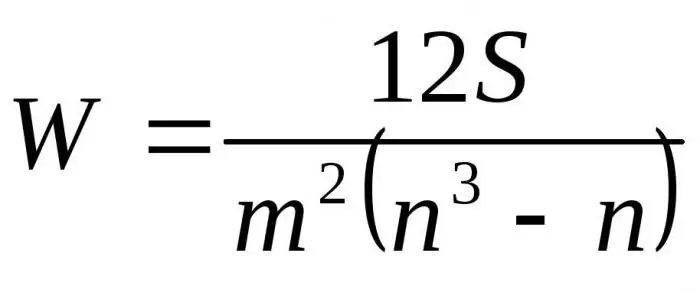
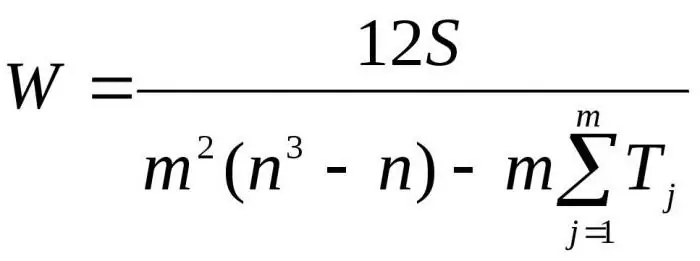
Itt m a szakértők száma, n az objektumok száma.
Az első képlet a konkordanciatényező meghatározására szolgál, ha nincsenek kapcsolódó rangok. A második képletet akkor használjuk, ha vannak kapcsolódó rangok.
Tehát a konkordancia együttható számításának vége. Mi a következő lépés? A kapott érték szignifikancia-értékelése a Pearson-együttható segítségével történik úgy, hogy ezt az együtthatót megszorozzuk a szakértők számával és a szabadságfokok számával (m-1). A kapott kritériumot összehasonlítjuk a táblázat értékével, és ha az első értéke meghaladja az utolsót, akkor a vizsgált együttható jelentőségéről beszélnek.
A rokon rangok esetében a Pearson-kritérium kiszámítása némileg bonyolultabbá válik, és a következő arány szerint történik: (12S)/(d(m2+ m)-(1/(m-1))x(Ts1 +Ts2 +Tsn)
Példa
Tegyük fel, hogy a szakértői módszer a kiskereskedelmi hálózatban értékesített vaj versenyképességét értékeli. Adjunk példát a konkordancia együttható kiszámítására. A versenyképesség értékelése előtt a fogyasztót rangsorolni kella termék azon tulajdonságait, amelyek az értékelésben részt vesznek. Tegyük fel, hogy ezek a tulajdonságok a következők lesznek: íz és illat, állag és megjelenés, szín, csomagolás és címkézés, zsírtartalom, kereskedelmi név, gyártó, ár.
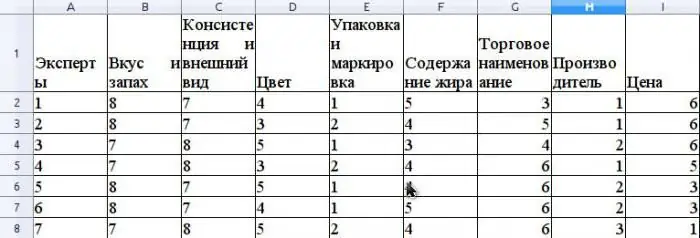
Tegyük fel, hogy a szakértői csoport 7 szakértőből áll. Az ábra ezen tulajdonságok rangsorolásának eredményeit mutatja.
R átlagértékét a rendszer a számtani átlagként számítja ki, és 31,5 lesz. S megtalálásához összegezze az ris és r átlag közötti különbségek négyzetét a képlet szerint. fent, és határozza meg, hogy S értéke 1718.
Számítsa ki a konkordancia együtthatót a képlet segítségével a kapcsolódó rangok használata nélkül (a rangok akkor lennének kapcsolatban, ha ugyanaz az Expert Advisor különböző tulajdonságokhoz ugyanazokkal a rangokkal rendelkezik).
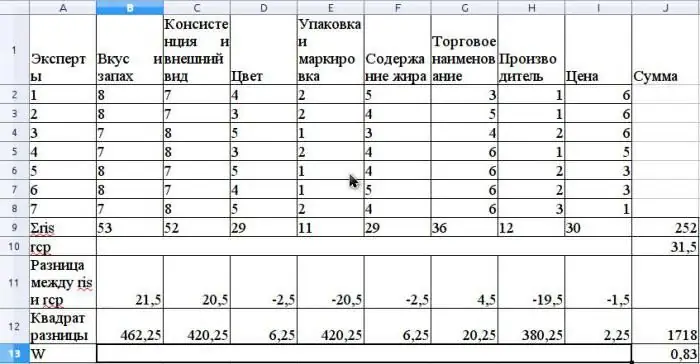
Ennek az együtthatónak az értéke 0,83 lesz. Ez erős konszenzusra utal a szakértők között.
Ellenőrizze jelentőségét a Pearson-teszt segítségével:
7 x 0,83 x (8-1)=40,7.
Pearson táblázatos tesztje 1%-os szignifikanciaszinten 18,5, 5%-nál pedig 14,1..
A példa bemutatja a számítás egyszerűségét és hozzáférhetőségét minden olyan személy számára, aki ismeri a matematikai számítások alapjait. Ezek enyhítésére,használjon táblázatos űrlapokat.
Befejezésül
Így a konkordancia együtthatója több szakértő véleményének konzisztenciáját mutatja. Minél távolabb van a 0-tól és közelebb van az 1-hez, annál következetesebbek a vélemények. Ezeket az együtthatókat a Pearson-kritérium kiszámításával kell megerősíteni.






