A gázokat a termodinamika szempontjából makroszkopikus jellemzők halmaza írja le, amelyek közül a legfontosabb a hőmérséklet, nyomás és térfogat. Ezen paraméterek egyikének állandósága és a másik kettő változása azt jelzi, hogy egyik vagy másik izofolyamat játszódik le a gázban. Ezt a cikket azoknak a kérdéseknek a részletes megválaszolásának szenteljük, hogy ez egy izochor folyamat, miben különbözik a gázrendszer állapotának izoterm és izobár változásaitól.
Ideális gáz a fizikában

Mielőtt arra a kérdésre válaszolna, hogy ez izochor folyamat, érdemes jobban megismerni az ideális gáz fogalmát. A fizikában minden olyan gázt értünk, amelyben az alkotó részecskéinek átlagos kinetikus energiája jóval meghaladja a kölcsönhatásuk potenciális energiáját, és e részecskék közötti távolságok több nagyságrenddel nagyobbak, mint lineáris méreteik. A megjelölt feltételek mellett kivitelezéskor lehetségesa számítások nem veszik figyelembe a részecskék közötti kölcsönhatási energiát (ez egyenlő nullával), és az is feltételezhető, hogy a részecskék bizonyos m tömegű anyagi pontok.
Az egyetlen folyamat, amely ideális gázban megy végbe, az a részecskék ütközése az anyagot tartalmazó edény falával. Ezek az ütközések a gyakorlatban a P gázban egy bizonyos nyomás fennállásaként nyilvánulnak meg.
Általában minden gáznemű anyag, amely kémiailag viszonylag közömbös molekulákból áll, alacsony nyomású és magas hőmérsékletű, ideális gáznak tekinthető, kellő pontossággal a gyakorlati számításokhoz.
Az ideális gázt leíró egyenlet
Természetesen Clapeyron-Mengyelejev univerzális törvényéről beszélünk, amelyet jól meg kell érteni ahhoz, hogy megértsük, ez egy izokorikus folyamat. Tehát az egyetemes állapotegyenletnek a következő alakja van:
PV=nRT.
Azaz a P nyomás és a V gáztérfogat szorzata egyenlő a T abszolút hőmérséklet és az n molban kifejezett anyagmennyiség szorzatával, ahol R az arányossági tényező. Magát az egyenletet először Emile Clapeyron írta le 1834-ben, és a 19. század 70-es éveiben D. Mengyelejev lecserélte benne egyetlen univerzális gázállandó R (8,314 J/(molK) állandó értékeinek halmazát.)).
A Clapeyron-Mendeleev egyenletnek megfelelően egy zárt rendszerben a gázrészecskék száma állandó marad, így csak három makroszkopikus paraméter változhat (T, Pés V). Ez utóbbi tény alapozza meg a különféle izofolyamatok megértését, amelyekről az alábbiakban lesz szó.
Mi az izokhorikus folyamat?
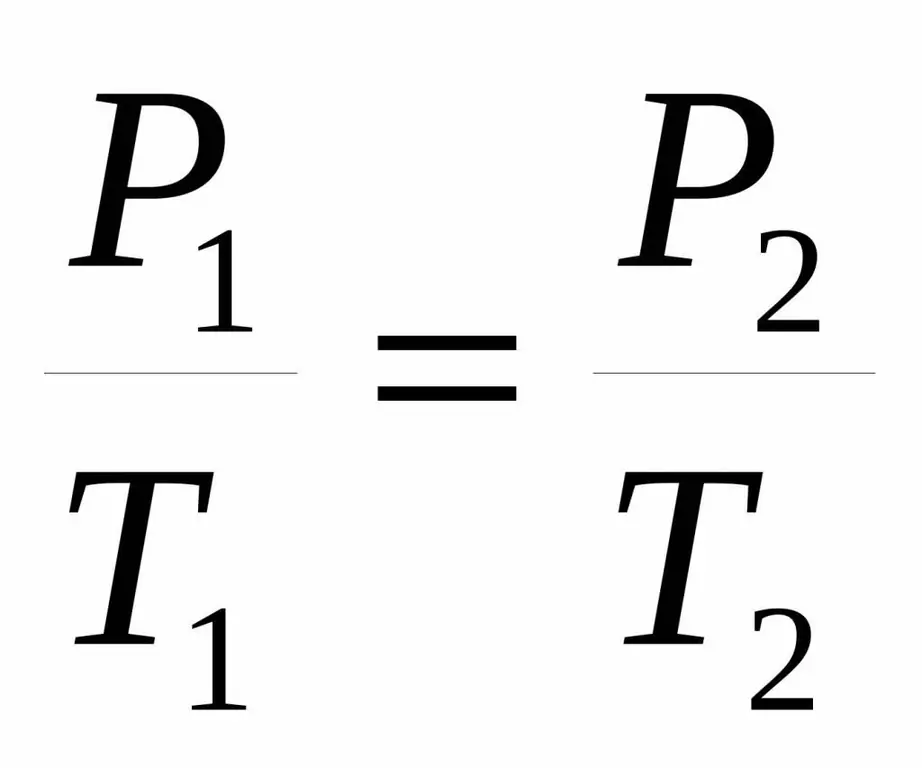
Ezen a folyamaton a rendszer állapotának minden olyan változását értjük, amelyben a térfogata megmarad.
Ha rátérünk az univerzális állapotegyenletre, akkor azt mondhatjuk, hogy izokorikus folyamatban csak a nyomás és az abszolút hőmérséklet változik a gázban. A termodinamikai paraméterek pontos változásának megértéséhez írjuk a megfelelő matematikai kifejezést:
P / T=állandó
Néha ez az egyenlőség kissé eltérő formában adható meg:
P1 / T1=P2 / T 2.
Mindkét egyenlőséget Károly törvényének nevezik egy francia tudós nevéről, aki a 18. század végén kísérleti úton szerezte meg az említett függőséget.

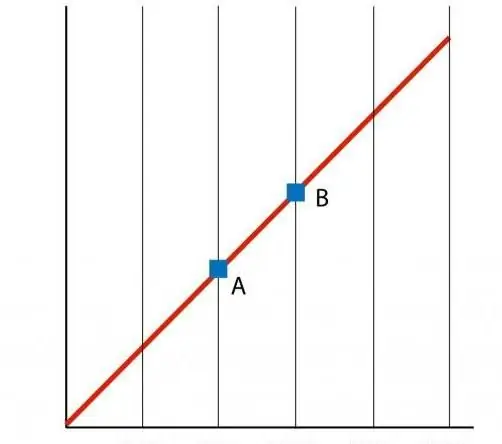
Ha felállítjuk a P(T) függvény grafikonját, akkor egy egyenes függőséget kapunk, amit izohornak nevezünk. Bármely izokor (n és V összes értékére) egyenes.
A folyamat energetikai leírása
Mint megjegyeztük, az izokhorikus folyamat egy rendszer állapotának megváltozása, amely zárt, de nem elszigetelt rendszerben megy végbe. A gáz és a környezet közötti hőcsere lehetőségéről beszélünk. Általánosságban elmondható, hogy a rendszer bármely Q hőellátása két eredményhez vezet:
- megváltoztatja a belső energiát U;
- gázdolgozik A, bővíti vagy összehúzza.
Az utolsó következtetést matematikailag a következőképpen írjuk le:
Q=U + A.
Az ideális gáz izokhorikus folyamata definíciója szerint nem jelenti a gáz által végzett munkát, mivel térfogata változatlan marad. Ez azt jelenti, hogy a rendszerbe szállított összes hő a belső energia növelésére megy el:
Q=U.
Ha ebbe a kifejezésbe behelyettesítjük a belső energia explicit képletét, akkor az izokhorikus folyamat hője a következőképpen ábrázolható:
Q=z / 2nRT.
Itt z a szabadsági fokok száma, amelyet a gázt alkotó molekulák többatomos természete határoz meg. Egyatomos gáz esetén z=3, kétatomos gáz esetén - 5, háromatomos és több atom esetén - 6. Itt a szabadsági fok alatt transzlációs és forgási fokokat értünk.
Ha összehasonlítjuk egy gázrendszer fűtésének hatásfokát izokoros és izobár folyamatokban, akkor az első esetben kapjuk a maximális hatásfokot, hiszen a rendszer izobár állapotváltozása során a gáz kitágul, ill. a hőbevitel egy részét munkára fordítják.
Izobár folyamat
Fentebb részletesen leírtuk, hogy ez egy izokhorikus folyamat. Most pedig ejtsünk néhány szót más izofolyamatokról. Kezdjük az izobárral. Az elnevezés alapján a rendszer állandó nyomású állapotok közötti átmenetét értjük. Ezt a folyamatot a Gay-Lussac törvény a következőképpen írja le:
V / T=konst.
Az izokorhoz hasonlóan a V(T) izosáv is egy egyenest jelöl a grafikonon.
AzértBármely izobár folyamat esetében célszerű kiszámítani a gáz által végzett munkát, mivel az egyenlő az állandó nyomás és a térfogatváltozás szorzatával.
Izotermikus folyamat
Ez egy olyan folyamat, amelyben a rendszer hőmérséklete állandó marad. A Boyle-Mariotte törvény ideális gázra írja le. Érdekes megjegyezni, hogy ez az első kísérletileg felfedezett gáztörvény (17. század második fele). A matematikai jelölése így néz ki:
PV=állandó
Izochor és izoterm folyamatok grafikus ábrázolásukat tekintve különböznek, mivel a P(V) függvény hiperbolikus, nem lineáris összefüggés.
Példa problémamegoldásra
Konszolidáljuk a cikkben közölt elméleti információkat alkalmazásukkal egy gyakorlati probléma megoldására. Ismeretes, hogy tiszta gáz-halmazállapotú nitrogén volt egy hengerben 1 atmoszféra nyomáson és 25 °C hőmérsékleten. A gázpalack felmelegítése és a benne lévő nyomás mérése után kiderült, hogy 1,5 atmoszféra. Mekkora a gáz hőmérséklete a hengerben melegítés után? Mennyivel változott a gáz belső energiája, ha 4 mol nitrogén volt a ballonban.
Az első kérdés megválaszolásához a következő kifejezést használjuk:
P1 / T1=P2 / T 2.
Ahonnan:
T2=P2 / P1 T 1.
Ebben a kifejezésben a nyomás tetszőleges mértékegységekkel helyettesíthetőmérések, mivel zsugorodnak, és a hőmérséklet csak kelvinben van megadva. Ezzel a következőt kapjuk:
T2=1,5 /1298,15=447,224 K.
A számított hőmérséklet Celsius-fokban 174 °C.
Mivel a nitrogénmolekula kétatomos, belső energiájának melegítés közbeni változása a következőképpen határozható meg:
ΔU=5/2nRΔT.
Ebbe a kifejezésbe behelyettesítve az ismert értékeket, megkapjuk a választ a feladat második kérdésére: ΔU=+12,4 kJ.






